Bài 7 trang 132 SGK Toán 8 tập 2

   Lời giải bài 7 trang 132 sgk Toán 8 tập 2 được chia sẻ với mục đích tham khảo cách làm và so sánh đáp án. Cùng với đó góp phần giúp bạn ôn tập lại các kiến thức Toán 8 phần hình học để tự tin hoàn thành tốt các bài tập nâng cao khác.

Đề bài 7 trang 132 SGK Toán 8 tập 2

Cho tam giác \(ABC\; (AB < AC)\). Tia phân giác của góc \(A\) cắt \(BC\) ở \(K\). Qua trung điểm \(M\) của \(BC\) kẻ một tia song song với \(KA\) cắt đường thẳng \(AB\) ở \(D\), cắt \(AC\) ở \(E\). Chứng minh \(BD = CE\).

» Bài tập trước: Bài 6 trang 132 SGK Toán 8 tập 2

Giải bài 7 trang 132 sgk Toán 8 tập 2

Hướng dẫn cách làm

Áp dụng: Tính chất đường phân giác, tính chất hai tam giác đồng dạng.

Bài giải chi tiết

Dưới đây là các cách giải bài 7 trang 132 SGK Toán 8 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

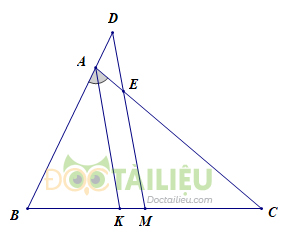
\(AK\) là đường phân giác của tam giác \(ABC\) (gt) nên

\(\dfrac{{KB}}{{AB}} = \dfrac{{KC}}{{AC}}\) (1) (tính chất đường phân giác của tam giác)

Vì \(MD // AK\)  (gt)nên: 

\(∆ABK  ∽ ∆DBM\) và \(∆ECM  ∽ ∆ACK\)

Do đó:

\(\dfrac{{KB}}{{AB}} = \dfrac{{BM}}{{BD}}\)   (2) và \( \dfrac{{CM}}{{CE}} = \dfrac{{KC}}{{AC}}\) (3) (tính chất hai tam giác đồng dạng)

Từ (1), (2) và (3) ta có: \(\dfrac{{BM}}{{BD}} = \dfrac{{CM}}{{CE}}\) (4)

Do \(BM = CM\) (vì \(M\) là trung điểm) nên từ (4) suy ra: \(BD = CE.\)

» Bài tập tiếp theo: Bài 8 trang 132 SGK Toán 8 tập 2

   Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 7 trang 132 sgk toán 8 tập 2. Mong rằng những bài hướng dẫn giải toán 8 của Đọc Tài Liệu sẽ là người đồng hành giúp các bạn học tốt môn học này.