Bài 11 trang 132 SGK Toán 8 tập 2

Lời giải bài 11 trang 132 sgk Toán 8 tập 2 được chia sẻ với mục đích tham khảo cách làm và so sánh đáp án. Cùng với đó góp phần giúp bạn ôn tập lại các kiến thức Toán 8 phần hình học để tự tin hoàn thành tốt các bài tập nâng cao khác.

Đề bài 11 trang 132 SGK Toán 8 tập 2

Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy $AB = 20\, cm$, cạnh bên $SA = 24\,cm.$

a) Tính chiều cao $SO$ rồi tính thể tích của hình chóp.

b) Tính diện tích toàn phần của hình chóp.

» Bài tập trước: Bài 10 trang 132 SGK Toán 8 tập 2

Giải bài 11 trang 132 sgk Toán 8 tập 2

Hướng dẫn cách làm

Áp dụng công thức tính thể tích và diện tích toàn phần của hình chóp tứ giác đều.

Bài giải chi tiết

Dưới đây là các cách giải bài 11 trang 132 SGK Toán 8 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

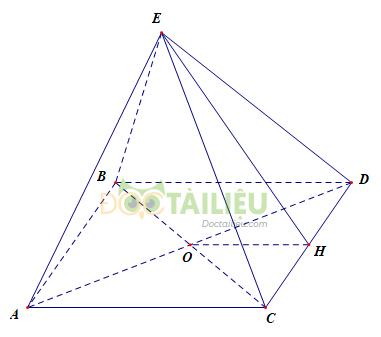
a) Vì $S.ABCD$ là hình chóp tứ giác đều nên $ABCD$ là hình vuông.

Do đó, $B{\rm{D}} = AB\sqrt 2  = 20\sqrt 2 \,cm$

Vì $SO$ là đường cao nên $SO \bot \left( {ABC{\rm{D}}} \right)$ hay $\Delta {\rm{OSD}}$ vuông tại $O.$

Áp dụng định lí Pitago ta có:

$S{O^2} = S{D^2} - O{D^2}$$\,= {24^2} - {\left( {\dfrac{{20\sqrt 2 }}{2}} \right)^2}$ $= 376$

$\Rightarrow SO \approx 19,4\left( {cm} \right)$

$V =\dfrac{1}{3}{.20^2}.19,4\approx 2586,7$ (cm²)

b) Gọi $H$ là trung điểm của $CD$.

$S{H^2} = S{D^2} - D{H^2} = {24^2} - {\left( {\dfrac{{20}}{2}} \right)^2}$ $= 476$

$\Rightarrow SH  ≈ 21,8 (cm)$

${S_{xq}} = p.d = \dfrac{1}{2}.4.20.21,8=872$ (cm²)

${S_đ} = A{B^2} = {20^2} = 400\left( {c{m^2}} \right)$

${S_{tp}} = {S_{xq}} + {S_đ} = 872 + 400 = 1272$ ${\left( {cm} \right)^2}$

Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 11 trang 132 sgk toán 8 tập 2. Mong rằng những bài hướng dẫn giải toán 8 của Đọc Tài Liệu sẽ là người đồng hành giúp các bạn học tốt môn học này.