Bài 63 trang 100 SGK Toán 8 tập 1

Tài liệu hướng dẫn giải bài 63 trang 100 sgk Toán 8 tập 1 này giúp bạn biết được cách làm để hoàn thành tốt bài tập và nắm vững các kiến thức quan trọng của chương 1 phần hình học hình chữ nhật đã được học trên lớp.

Đề bài 63 trang 100 SGK Toán 8 tập 1

Tìm $x$ trên hình $90$

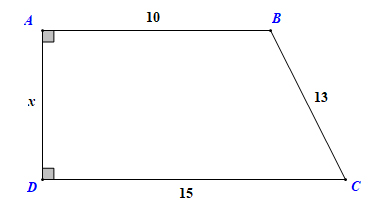
» Bài tập trước: Bài 62 trang 100 sgk Toán 8 tập 1

Giải bài 63 trang 100 sgk Toán 8 tập 1

Hướng dẫn cách làm

Áp dụng:

• + Dấu hiệu nhận biết hình chữ nhật: Tứ giác có ba góc vuông là hình chữ nhật.
• + Định lí Pytago: Bình phương cạnh huyền bằng tổng các bình phương hai cạnh góc vuông.

Bài giải chi tiết

Dưới đây là các cách giải bài 63 trang 100 SGK Toán 8 tập 1 để các bạn tham khảo và so sánh bài làm của mình:

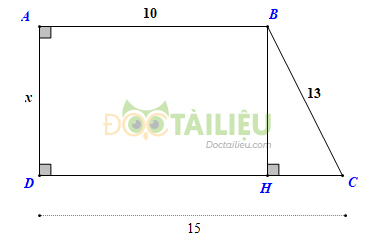
Kẻ $BH ⊥ CD$

Tứ giác $ABHD$ có $\widehat A = \widehat D = \widehat H = {90^0}$ (giả thiết)

$\Rightarrow$  Tứ giác $ABHD$ là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)

$\Rightarrow  DH =AB= 10$ (tính chất hình chữ nhật)

Ta có:  $HC = DC - DH = 15-10=5.$

Áp dụng định lí Pytago vào tam giác vuông $BHC$ vuông tại $H$ ta có:

$\eqalign{ & B{H^2} = B{C^2} - H{C^2} = {13^2} - {5^2} \cr&\;\;\;\;\;\;\;\;\;= 169 - 25 = 144 \cr & BH = x = \sqrt {144} = 12 \cr}$

Vậy  $x = 12$.

» Bài tập tiếp theo: Bài 64 trang 100 sgk Toán 8 tập 1

Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 63 trang 100 sgk toán 8 tập 1. Mong rằng những bài hướng dẫn giải toán 8 của Đọc Tài Liệu sẽ là người đồng hành giúp các bạn học tốt môn học này.