Bài 20 trang 68 SGK Toán 8 tập 2

Lời giải bài 20 trang 68 sgk Toán 8 tập 2 được chia sẻ với mục đích tham khảo cách làm và so sánh đáp án. Cùng với đó góp phần giúp bạn ôn tập lại các kiến thức Toán 8 chương 3 phần hình học để tự tin hoàn thành tốt các bài tập về tính chất đường phân giác của tam giác khác.

Đề bài 20 trang 68 SGK Toán 8 tập 2

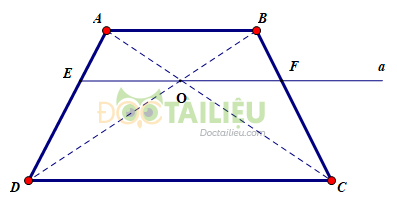
Cho hình thang \(ABCD\; (AB //CD)\). Hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Đường thẳng \(a\) qua \(O\) và song song với đáy của hình thang cắt các cạnh \(AD, BC\) theo thứ tự \(E\) và \(F\) (h26)

Chứng minh rằng \(OE = OF\).

» Bài tập trước: Bài 19 trang 68 sgk Toán 8 tập 2

Giải bài 20 trang 68 sgk Toán 8 tập 2

Hướng dẫn cách làm

- Áp dụng hệ quả của định lí TaLet trong tam giác.

Bài giải chi tiết

Dưới đây là các cách giải bài 20 trang 68 SGK Toán 8 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

\(∆ADC\) có \(OE // DC\) (gt) nên \(\dfrac{OE}{DC} = \dfrac{AE}{AD}\)  (1) (hệ quả của định lí TaLet trong tam giác)

\(∆BDC\) có \(OF // DC\) (gt) nên \(\dfrac{OF}{DC} = \dfrac{BF}{BC}\)   (2) (hệ quả của định lí TaLet trong tam giác)

Mà \(AB // CD\) (gt) nên \(\dfrac{AE}{AD} = \dfrac{BF}{BC}\) (theo câu b bài 19)   (3)

Từ (1), (2), (3) suy ra \(\dfrac{OE}{DC} = \dfrac{OF}{DC}\) nên \(OE = OF\).

» Bài tập tiếp theo: Bài 21 trang 68 sgk Toán 8 tập 2

Video giải bài 20 trang 68 SGK Toán 8 tập 2

Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 20 trang 68 sgk toán 8 tập 2. Mong rằng những bài hướng dẫn giải toán 8 của Đọc Tài Liệu sẽ là người đồng hành giúp các bạn học tốt môn học này.