Bạn đang tìm kiếm tài liệu tổng hợp kiến thức về đường phân giác của tam giác? Hãy tham khảo ngay bài viết dưới đây của Đọc tài liệu với những lý thuyết Tính chất đường phân giác của tam giác cùng tổng hợp các dạng toán cơ bản thường gặp. Đây sẽ là tài liệu học tập hữu ích cho học sinh và đồng thời giúp các thầy cô có thêm tài liệu hay phục vụ việc dạy học.
Cùng tham khảo nhé!

I. Lý thuyết Tính chất đường phân giác của tam giác
Chú ý: Định lí vẫn đúng với tia phân giác của góc ngoài của tam giác.
Ví dụ: Cho tam giác \(ABC\) có \(AD,\,AE\) lần lượt là đường phân giác góc trong và góc ngoài tại đỉnh \(A\) .
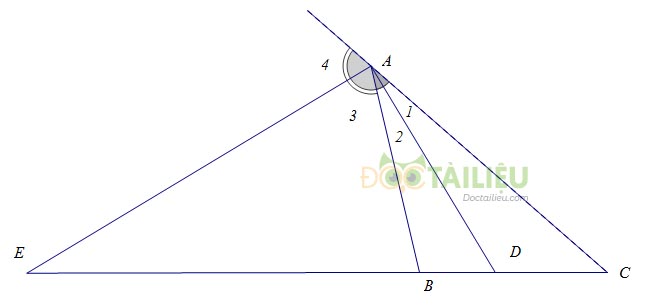
Khi đó ta có \(\dfrac{{DB}}{{DC}} = \dfrac{{AB}}{{AC}}\) và \( \dfrac{{EB}}{{EC}} = \dfrac{{AB}}{{AC}}\)
II. Các dạng toán thường gặp
Dạng 1: Tính độ dài cạnh, chu vi, diện tích
Phương pháp:
Sử dụng tính chất đường phân giác của tam giác và tỉ lệ thức để biến đổi và tính toán.
+ Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hoai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
Dạng 2: Chứng minh đẳng thức hình học và các bài toán khác
Phương pháp:
Sử dụng tính chất đường phân giác của tam giác: “Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hoai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.”
III. Bài tập mẫu về Tính chất đường phân giác của tam giác
Tam giác cân \(BAC\) có \(BA = BC = a, AC = b.\) Đường phân giác góc \(A \)cắt \(BC\) tại \(M\), đường phân giác góc \(C\) cắt \(BA\) tại \(N\)
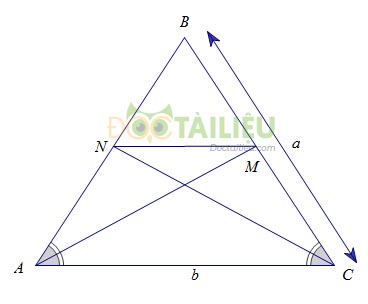
a) Chứng minh rằng: \( MN // AC.\)
b) Tính \(MN\) theo \(a, b\)
Lời giải
a) Xét \(\Delta BAC\) có \(AM\) là đường phân giác của \(\widehat {BAC}\)
\(\Rightarrow \displaystyle{{MC} \over {MB}} = {{AC} \over {AB}}\) (tính chất đường phân giác ) (1)
\(CN\) là đường phân giác của \(\widehat {BCA}\)
\(\Rightarrow \displaystyle{{NA} \over {NB}} = {{AC} \over {BC}}\) (tính chất đường phân giác ) (2)
Lại có: \(AB = CB = a\) (gt) (3)
Từ (1), (2) và (3) suy ra: \(\displaystyle {{MC} \over {MB}} = {{NA} \over {NB}}\)
Xét \(\Delta BAC\) có \(\displaystyle {{MC} \over {MB}} = {{NA} \over {NB}}\) nên theo định lí đảo của định lí Ta-lét ta có \(MN // AC\).
b) Ta có: \(\displaystyle {{MC} \over {MB}} = {{AC} \over {AB}}\) (chứng minh trên )
\(\Rightarrow \dfrac{{MC}}{{MB}} + 1 = \dfrac{{AC}}{{AB}} + 1\) \(\Rightarrow \displaystyle {{MC + MB} \over {MB}} = {{AC + AB} \over {AB}} \) \(\Rightarrow \displaystyle {{CB} \over {MB}} = {{AC + AB} \over {AB}}\) \(\Rightarrow \displaystyle{a \over {MB}} = {{b + a} \over a}\) \(\Rightarrow \displaystyle MB = {{{a^2}} \over {a + b}}\)
Xét \(\Delta BAC\) có \(MN // AC\) (chứng minh trên)
Theo hệ quả của định lí Ta-lét ta có: \(\displaystyle {{MN} \over {AC}} = {{MB} \over {BC}}\)
\( \Rightarrow MN = \dfrac{{AC.MB}}{{BC}} = \dfrac{{b.\dfrac{{{a^2}}}{{a + b}}}}{a} \)\(\,= \dfrac{{ab}}{{a + b}}\)
****************
Hy vọng với hệ thống kiến thức lý thuyết Tính chất đường phân giác của tam giác trên đây, các em sẽ có thêm một tài liệu học tập hữu ích để học tốt hơn môn Toán 8. Chúc các em luôn học tốt và đạt kết quả cao!