Bài 1 trang 9 sgk toán 7 tập 1 chân trời sáng tạo
Câu hỏi
Thay ? bằng kí hiệu \( \in ,\, \notin \) thích hợp

Bài giải
\(\begin{array}{l} - 7 \notin \mathbb{N};\,\,\,\,\,\,\, - 17 \in \mathbb{Z};\,\,\,\,\,\,\,\,\,\,\, - 38 \in Q\\\frac{4}{5} \notin \mathbb{Z};\,\,\,\,\,\,\,\,\,\,\,\frac{4}{5} \in \mathbb{Q};\,\,\,\,\,\,\,\,\,\,\,\,\,\,0,25 \notin \mathbb{Z};\,\,\,\,\,3,25 \in Q\end{array}\)
Bài 2 trang 9 sgk toán 7 tập 1 chân trời sáng tạo
Câu hỏi
a) Trong các số sau, những phân số nào biểu diễn số hữu tỉ \(\frac{{ - 5}}{9}\)?
\(\frac{{ - 10}}{{18}};\,\frac{{10}}{{18}};\,\frac{{15}}{{ - 27}};\, - \frac{{20}}{{36}};\,\frac{{ - 25}}{{27}}.\)
b) Tìm số đối của mỗi số sau: \(12;\,\frac{{ 4}}{9};\, - 0,375;\,\frac{0}{5};\,-2\frac{2}{5}.\)
Bài giải
a) Ta có:
\(\begin{array}{l}\frac{{ - 10}}{{18}} = \frac{{ - 5}}{9};\,\,\,\\\frac{{10}}{{18}} = \frac{5}{9};\,\,\\\,\frac{{15}}{{ - 27}} = \frac{{ - 5}}{9};\,\\ - \frac{{20}}{{36}} = \frac{{ - 5}}{9}.\end{array}\)
Vậy những phân số nào biểu diễn số hữu tỉ \(\frac{{ - 5}}{9}\) là: \(\frac{{ - 10}}{{18}};\,\frac{{15}}{{ - 27}};\, - \frac{{20}}{{36}}.\)
b) Số đối của các số \(12;\,\frac{{ 4}}{9};\, - 0,375;\,\frac{0}{5};\,-2\frac{2}{5}\) lần lượt là: \( - 12;\,\frac{-4}{9};\,0,375;\,\frac{0}{5};\, 2\frac{2}{5}\).
Bài 3 trang 9 sgk toán 7 tập 1 chân trời sáng tạo
Câu hỏi
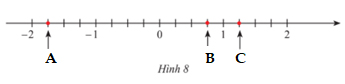
a) Các điểm A,B,C trong Hình 8 biểu diễn số hữu tỉ nào?
b) Biểu diễn các số hữu tỉ \(\frac{{ - 2}}{5};\,1\frac{1}{5};\,\frac{3}{5};\, - 0,8\) trên trục số.
Bài giải
a) Các điểm A,B,C trong Hình 8 biểu diễn lần lượt các số hữu tỉ: \(\frac{{ - 7}}{4};\,\frac{3}{4};\,\frac{5}{4}.\)
b) Ta có: \(1\frac{1}{5} = \frac{6}{5};\,\,\, - 0,8 = \frac{{ - 8}}{{10}} = \frac{{ - 4}}{5}.\)
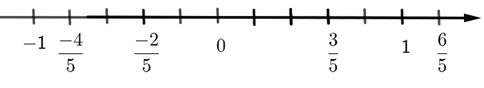
Bài tiếp theo: Trang 10 SGK Toán 7 tập 1 Chân trời sáng tạo
Xem thêm:
- Trang 15 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 16 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 20 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 21 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 25 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 27 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 28 SGK Toán 7 tập 1 Chân trời sáng tạo
Trên đây là chi tiết hướng dẫn Giải bài tập Trang 9 SGK Toán 7 tập 1 Chân trời sáng tạo được Đọc Tài Liệu biên soạn với mong muốn hỗ trợ các em học sinh học tốt hơn môn Toán lớp 7
Hướng dẫn giải Toán 7 Chân trời sáng tạo bởi Đọc Tài Liệu