Bài 1 trang 27 sgk toán 7 tập 1 chân trời sáng tạo
Câu hỏi
Thực hiện phép tính.
a)\(\frac{2}{5} + \frac{3}{5}:\left( { - \frac{3}{2}} \right) + \frac{1}{2};\)
b)\(2\frac{1}{3} + {\left( { - \frac{1}{3}} \right)^2} - \frac{3}{2};\)
c)\(\left( {\frac{7}{8} - 0,25} \right):{\left( {\frac{5}{6} - 0,75} \right)^2};\)
d)\(\left( { - 0,75} \right) - \left[ {\left( { - 2} \right) + \frac{3}{2}} \right]:1,5 + \left( {\frac{{ - 5}}{4}} \right)\)
Bài giải
a)
\(\begin{array}{l}\frac{2}{5} + \frac{3}{5}:\left( { - \frac{3}{2}} \right) + \frac{1}{2}\\ = \frac{2}{5} + \frac{3}{5}.\left( {\frac{{ - 2}}{3}} \right) + \frac{1}{2}\\ = \frac{2}{5} + \frac{{ - 2}}{5} + \frac{1}{2}\\ = \frac{1}{2}\end{array}\)
b)
\(\begin{array}{l}2\frac{1}{3} + {\left( { - \frac{1}{3}} \right)^2} - \frac{3}{2}\\ = \frac{7}{3} + \frac{1}{9} - \frac{3}{2}\\ = \frac{{42}}{{18}} + \frac{2}{{18}} - \frac{{27}}{{18}}\\ = \frac{{17}}{{18}}\end{array}\)
c)
\(\begin{array}{l}\left( {\frac{7}{8} - 0,25} \right):{\left( {\frac{5}{6} - 0,75} \right)^2}\\ = \left( {\frac{7}{8} - \frac{1}{4}} \right):\left( {\frac{5}{6} - \frac{3}{4}} \right)^2\\ = \left( {\frac{7}{8} - \frac{2}{8}} \right):\left( {\frac{{10}}{{12}} - \frac{9}{{12}}} \right)^2\\ = \frac{5}{8}:(\frac{1}{{12}})^2\\ =\frac{5}{8}:\frac{1}{144}\\= \frac{5}{8}.144\\ = 90\end{array}\)
d)
\(\begin{array}{l}\left( { - 0,75} \right) - \left[ {\left( { - 2} \right) + \frac{3}{2}} \right]:1,5 + \left( {\frac{{ - 5}}{4}} \right)\\ = \left( {\frac{{ - 3}}{4}} \right) - \left[ {\frac{{ - 4}}{2} + \frac{3}{2}} \right]:\frac{3}{2} + \left( {\frac{{ - 5}}{4}} \right)\\ = \left( {\frac{{ - 3}}{4}} \right) - \frac{{ - 1}}{2}.\frac{2}{3} + \left( {\frac{{ - 5}}{4}} \right)\\ = \left( {\frac{{ - 3}}{4}} \right) + {\frac{{ 1}}{3}} + \frac{-5}{4}\\= \left( {\frac{{ - 3}}{4}} \right) + \left( {\frac{{ - 5}}{4}} \right) + \frac{1}{3}\\ = - 2 + \frac{1}{3}\\ = \frac{{ - 6}}{3} + \frac{1}{3}\\ = \frac{{ - 5}}{3}\end{array}\)
Bài 2 trang 27 sgk toán 7 tập 1 chân trời sáng tạo
Câu hỏi
Thực hiện phép tính (bằng cách hợp lí nếu có thể).
a)\(\frac{5}{{23}} + \frac{7}{{17}} + 0,25 - \frac{5}{{23}} + \frac{{10}}{{17}}\)
b)\(\frac{3}{7}.2\frac{2}{3} - \frac{3}{7}.1\frac{1}{2};\)
c)\(13\frac{1}{4}:\left( { - \frac{4}{7}} \right) - 17\frac{1}{4}:\left( { - \frac{4}{7}} \right);\)
d)\(\frac{{100}}{{123}}:\left( {\frac{3}{4} + \frac{7}{{12}}} \right) + \frac{{23}}{{123}}:\left( {\frac{9}{5} - \frac{7}{{15}}} \right).\)
Bài giải
a)
\(\begin{array}{l}\frac{5}{{23}} + \frac{7}{{17}} + 0,25 - \frac{5}{{23}} + \frac{{10}}{{17}}\\ = \left( {\frac{5}{{23}} - \frac{5}{{23}}} \right) + \left( {\frac{7}{{17}} + \frac{{10}}{{17}}} \right) + 0,25\\ = 0 + \frac{{17}}{{17}} + \frac{{25}}{{100}}\\ = 1 + \frac{1}{4}\\ = \frac{5}{4}\end{array}\)
b)
\(\begin{array}{l}\frac{3}{7}.2\frac{2}{3} - \frac{3}{7}.1\frac{1}{2}\\ = \frac{3}{7}.\frac{8}{3} - \frac{3}{7}.\frac{3}{2}\\ = \frac{3}{7}.\left( {\frac{8}{3} - \frac{3}{2}} \right)\\ = \frac{3}{7}.\left( {\frac{{16}}{6} - \frac{9}{6}} \right)\\ = \frac{3}{7}.\frac{7}{6}\\ = \frac{1}{2}\end{array}\)
c)
\(\begin{array}{l}13\frac{1}{4}:\left( { - \frac{4}{7}} \right) - 17\frac{1}{4}:\left( { - \frac{4}{7}} \right)\\ = 13\frac{1}{4}.\frac{{ - 7}}{4} - 17\frac{1}{4}.\frac{{ - 7}}{4}\\ = \frac{{ - 7}}{4}.\left( {13\frac{1}{4} - 17\frac{1}{4}} \right)\\ = \frac{{ - 7}}{4}.\left( { - 4} \right)\\ = 7\end{array}\)
d)
\(\begin{array}{l}\frac{{100}}{{123}}:\left( {\frac{3}{4} + \frac{7}{{12}}} \right) + \frac{{23}}{{123}}:\left( {\frac{9}{5} - \frac{7}{{15}}} \right)\\ = \frac{{100}}{{123}}:\left( {\frac{9}{{12}} + \frac{7}{{12}}} \right) + \frac{{23}}{{123}}:\left( {\frac{{27}}{{15}} - \frac{7}{{15}}} \right)\\ = \frac{{100}}{{123}}:\frac{{16}}{{12}} + \frac{{23}}{{123}}:\frac{{20}}{{15}}\\ = \frac{{100}}{{123}}:\frac{4}{3} + \frac{{23}}{{123}}:\frac{4}{3}\\ = \frac{{100}}{{123}}.\frac{3}{4} + \frac{{23}}{{123}}.\frac{3}{4}\\ = \frac{3}{4}.\left( {\frac{{100}}{{123}} + \frac{{23}}{{123}}} \right)\\ = \frac{3}{4}.\frac{{123}}{{123}}\\ = \frac{3}{4}.1\\ = \frac{3}{4}\end{array}\)
Bài 3 trang 27 sgk toán 7 tập 1 chân trời sáng tạo
Câu hỏi
Thực hiện phép tính.
a) \(\frac{{{5^{16}}{{.27}^7}}}{{{{125}^5}{{.9}^{11}}}}\)
b)\({\left( { - 0,2} \right)^2}.5 - \frac{{{2^{13}}{{.27}^3}}}{{{4^6}{{.9}^5}}};\)
c)\(\frac{{{5^6} + {2^2}{{.25}^3} + {2^3}{{.125}^2}}}{{{{26.5}^6}}}.\)
Bài giải
a)
\(\frac{{{5^{16}}{{.27}^7}}}{{{{125}^5}{{.9}^{11}}}} = \frac{{{5^{16}}.{{\left( {{3^3}} \right)}^7}}}{{{{\left( {{5^3}} \right)}^5}.{{\left( {{3^2}} \right)}^{11}}}} = \frac{{{5^{16}}{{.3}^{21}}}}{{{5^{15}}{{.3}^{22}}}} = \frac{5.{{5^{15}}{{.3}^{21}}}}{{{5^{15}}{.3{.3}^{21}}}}= \frac{5}{3}\)
b)
\({\left( { - 0,2} \right)^2}.5 - \frac{{{2^{13}}{{.27}^3}}}{{{4^6}{{.9}^5}}} = 0,04.5 - \frac{{{2^{13}}.{{\left( {{3^3}} \right)}^3}}}{{{{\left( {{2^2}} \right)}^6}.{{\left( {{3^2}} \right)}^5}}}\\ = 0,2 - \frac{{{2^{13}}{{.3}^9}}}{{{2^{12}}{{.3}^{10}}}}\\ = \frac{1}{5} - \frac{2}{{3}} \\= \frac{3}{15} - \frac{10}{{15}}\\ = \frac{{-7}}{{15}}\)
c)
\(\begin{array}{l}\frac{{{5^6} + {2^2}{{.25}^3} + {2^3}{{.125}^2}}}{{{{26.5}^6}}} = \frac{{{5^6} + {2^2}.{{\left( {{5^2}} \right)}^3} + {2^3}.{{\left( {{5^3}} \right)}^2}}}{{{{2.13.5}^6}}}\\ = \frac{{{5^6} + {{4.5}^6} + {{8.5}^6}}}{{{{2.13.5}^6}}} = \frac{{{5^6}.\left( {1 + 4 + 8} \right)}}{{{{2.13.5}^6}}}\\ = \frac{{{5^6}.13}}{{{{2.13.5}^6}}} = \frac{1}{2}\end{array}\)
Bài 4 trang 27 sgk toán 7 tập 1 chân trời sáng tạo
Câu hỏi
Tính giá trị các biểu thức sau:
a)\(A = \left[ {\left( { - 0,5} \right) - \frac{3}{5}} \right]:\left( { - 3} \right) + \frac{1}{3} - \left( { - \frac{1}{6}} \right):\left( { - 2} \right)\)
b)\(B = \left( {\frac{2}{{25}} - 0,036} \right):\frac{{11}}{{50}} - \left[ {\left( {3\frac{1}{4} - 2\frac{4}{9}} \right)} \right].\frac{9}{{29}}\)
Bài giải
a)
\(\begin{array}{l}A = \left[ {\left( { - 0,5} \right) - \frac{3}{5}} \right]:\left( { - 3} \right) + \frac{1}{3} - \left( { - \frac{1}{6}} \right):\left( { - 2} \right)\\ = \left( {\frac{{ - 5}}{{10}} - \frac{6}{{10}}} \right).\frac{{ - 1}}{3} + \frac{1}{3} + \frac{1}{6}.\frac{{ - 1}}{2}\\ = \frac{{ - 11}}{{10}}.\frac{{ - 1}}{3} + \frac{1}{3} + \frac{1}{6}.\frac{{ - 1}}{2}\\ = \frac{{11}}{{30}} + \frac{1}{3} + \frac{{ - 1}}{{12}}\\ = \frac{{22}}{{60}} + \frac{{20}}{{60}} + \frac{{ - 5}}{{60}}\\ = \frac{{37}}{{60}}\end{array}\)
b)
\(\begin{array}{l}B = \left( {\frac{2}{{25}} - 0,036} \right):\frac{{11}}{{50}} - \left[ {\left( {3\frac{1}{4} - 2\frac{4}{9}} \right)} \right].\frac{9}{{29}}\\ = \left( {\frac{2}{{25}} - \frac{{36}}{{1000}}} \right).\frac{{50}}{{11}} - \left[ {\left( {\frac{{13}}{4} - \frac{{22}}{9}} \right)} \right].\frac{9}{{29}}\\ = \left( {\frac{{10}}{{125}} - \frac{4}{{125}}} \right).\frac{{50}}{{11}} - \left[ {\left( {\frac{{117}}{{36}} - \frac{{88}}{{36}}} \right)} \right].\frac{9}{{29}}\\ = \frac{{ - 6}}{{125}}.\frac{{50}}{{11}} - \frac{{29}}{{36}}.\frac{9}{{29}}\\ = \frac{{ - 12}}{{55}} - \frac{1}{4}\\ = \frac{{ - 48}}{{220}} - \frac{{55}}{{220}}\\ = \frac{{ - 103}}{{220}}\end{array}\)
Bài 5 trang 27 sgk toán 7 tập 1 chân trời sáng tạo
Câu hỏi
Tìm x, biết:
a)\( - \frac{3}{5}.x = \frac{{12}}{{25}};\)
b)\(\frac{3}{5}x - \frac{3}{4} = - 1\frac{1}{2};\)
c)\(\frac{2}{5} + \frac{3}{5}:x = 0,5;\)
d)\(\frac{3}{4} - \left( {x - \frac{1}{2}} \right) = 1\frac{2}{3}\)
e)\(2\frac{2}{{15}}:\left( {\frac{1}{3} - 5x} \right) = - 2\frac{2}{5}\)
g)\({x^2} + \frac{1}{9} = \frac{5}{3}:3.\)
Bài giải
a)
\(\begin{array}{l} - \frac{3}{5}.x = \frac{{12}}{{25}}\\x = \frac{{12}}{{25}}:\frac{{ - 3}}{5}\\x = \frac{{12}}{{25}}.\frac{{ - 5}}{3}\\x = \frac{{ - 4}}{5}\end{array}\)
Vậy \(x = \frac{{ - 4}}{5}\)
b)
\(\begin{array}{l}\frac{3}{5}x - \frac{3}{4} = - 1\frac{1}{2};\\\frac{3}{5}x = \frac{{ - 3}}{2} + \frac{3}{4}\\\frac{3}{5}x = \frac{{ - 3}}{4}\\x = \frac{{ - 3}}{4}:\frac{3}{5}\\x = \frac{{ - 3}}{4}.\frac{5}{3}\\x = \frac{{ - 5}}{4}\end{array}\)
Vậy \(x = \frac{{ - 5}}{4}\).
c)
\(\begin{array}{l}\frac{2}{5} + \frac{3}{5}:x = 0,5\\\frac{3}{5}:x = \frac{1}{2} - \frac{2}{5}\\\frac{3}{5}:x = \frac{1}{{10}}\\x = \frac{3}{5}:\frac{1}{{10}}\\x = \frac{3}{5}.10\\x = 6\end{array}\)
Vậy \(x = 6\).
d)
\(\begin{array}{l}\frac{3}{4} - \left( {x - \frac{1}{2}} \right) = 1\frac{2}{3}\\x - \frac{1}{2} = \frac{3}{4} - \frac{5}{3}\\x - \frac{1}{2} = \frac{{ - 11}}{{12}}\\x = \frac{{ - 11}}{{12}} + \frac{1}{2}\\x = \frac{{ - 5}}{{12}}\end{array}\)
Vậy \(x = \frac{{ - 5}}{{12}}\).
e)
\(\begin{array}{l}2\frac{2}{{15}}:\left( {\frac{1}{3} - 5x} \right) = - 2\frac{2}{5}\\\frac{{32}}{{15}}:\left( {\frac{1}{3} - 5x} \right) = - \frac{{12}}{5}\\\frac{1}{3} - 5x = \frac{{32}}{{15}}:\frac{{ - 12}}{5}\\\frac{1}{3} - 5x = \frac{{32}}{{15}}.\frac{{ - 5}}{12}\\\frac{1}{3} - 5x = \frac{{ - 8}}{9}\\5x = \frac{1}{3} + \frac{8}{9}\\5x = \frac{{11}}{9}\\x = \frac{{11}}{9}:5\\x = \frac{{11}}{{45}}\end{array}\)
Vậy \(x = \frac{{11}}{{45}}\).
g)
\(\begin{array}{l}{x^2} + \frac{1}{9} = \frac{5}{3}:3\\{x^2} + \frac{1}{9} = \frac{5}{9}\\{x^2} = \frac{5}{9} - \frac{1}{9}\\{x^2} = \frac{4}{9}\\{x^2} = (\pm\frac{2}{3})^2\\x = \pm \frac{2}{3}\end{array}\)
Vậy \(x = \pm \frac{2}{3}\).
Bài 6 trang 27 sgk toán 7 tập 1 chân trời sáng tạo
Câu hỏi
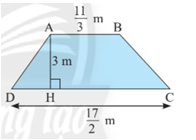
a) Tính diện tích hình thang ABCD có các kích thước như hình sau:
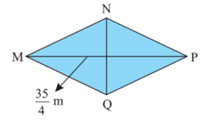
b) Hình thoi MNPQ có diện tích bằng diện tích hình thang ABCD ở câu a, đường chéo MP= \(\frac{{35}}{4}\)m. Tính độ dài NQ.
Bài giải
a) Diện tích hình thang là:
\(\dfrac{1}{2}.\left( {AB + DC} \right).AH = \dfrac{1}{2}.\left( {\dfrac{{11}}{3} + \dfrac{{17}}{2}} \right).3 = \dfrac{{73}}{4}\)(m2)
b) Ta có diện tích hình thoi MNPQ là \(\dfrac{{73}}{4}\,{m^2}\)
Nên ta có:
\(\begin{array}{ccccc}{S_{MNPQ}} =\dfrac{{73}}{4} \Rightarrow \dfrac{1}{2}.MP.NQ = \dfrac{{73}}{4}\\ \Rightarrow \dfrac{1}{2}.\dfrac{{35}}{4}.NQ = \dfrac{{73}}{4}\\ \Rightarrow \dfrac{{35}}{8}.NQ= \dfrac{{73}}{4} \Rightarrow NQ = \dfrac{{73}}{4}:\dfrac{{35}}{8} = \dfrac{{146}}{{35}}\end{array}\)
Vậy \(NQ = \dfrac{{146}}{{35}}\) m.
Bài tiếp theo: Trang 28 SGK Toán 7 tập 1 Chân trời sáng tạo
Xem thêm:
- Trang 9 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 10 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 15 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 16 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 20 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 21 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 25 SGK Toán 7 tập 1 Chân trời sáng tạo
Trên đây là chi tiết hướng dẫn Giải bài tập Trang 27 SGK Toán 7 tập 1 Chân trời sáng tạo được Đọc Tài Liệu biên soạn với mong muốn hỗ trợ các em học sinh học tốt hơn môn Toán lớp 7
Hướng dẫn giải Toán 7 Chân trời sáng tạo bởi Đọc Tài Liệu