Bài 1 trang 15 sgk toán 7 tập 1 chân trời sáng tạo
Câu hỏi
Tính:
a)\(\frac{2}{{15}} + \left( {\frac{{ - 5}}{{24}}} \right)\)
b) \(\left( {\frac{{ - 5}}{9}} \right) - \left( { - \frac{7}{{27}}} \right);\)
c)\(\left( { - \frac{7}{{12}}} \right) + 0,75\)
d)\(\left( {\frac{{ - 5}}{9}} \right) - 1,25\)
e)\(0,34.\frac{{ - 5}}{{17}}\)
g) \(\frac{4}{9}:\left( { - \frac{8}{{15}}} \right);\)
h)\(\left( {1\frac{2}{3}} \right):\left( {2\frac{1}{2}} \right)\)
i) \(\frac{2}{5}.\left( { - 1.25} \right)\)
k) \(\left( {\frac{{ - 3}}{5}} \right).\left( {\frac{{15}}{{ - 7}}} \right).3\frac{1}{9}\)
Bài giải
\(a)\frac{2}{{15}} + \left( {\frac{{ - 5}}{{24}}} \right) = \frac{{16}}{{120}} + \left( {\frac{{ - 25}}{{120}}} \right) = \frac{{ - 9}}{{120}} = \frac{{ - 3}}{{40}}\)
b) \(\left( {\frac{{ - 5}}{9}} \right) - \left( { - \frac{7}{{27}}} \right) = \left( {\frac{{ - 15}}{{27}}} \right) + \frac{7}{{27}} = \frac{{ - 8}}{{27}}\)
c)\(\left( { - \frac{7}{{12}}} \right) + 0,75 = \left( { - \frac{7}{{12}}} \right) + \frac{3}{4} = \left( { - \frac{7}{{12}}} \right) + \frac{9}{{12}} = \frac{2}{{12}} = \frac{1}{6}\)
d)\(\left( {\frac{{ - 5}}{9}} \right) - 1,25 = \left( {\frac{{ - 5}}{9}} \right) - \frac{5}{4} = \left( {\frac{{ - 20}}{{36}}} \right) - \frac{{45}}{{36}} = \frac{{ - 65}}{{36}}\)
e)\(0,34.\frac{{ - 5}}{{17}} = \frac{{17}}{{50}}.\frac{{ - 5}}{{17}} = \frac{{ - 1}}{{10}}\)
g) \(\frac{4}{9}:\left( { - \frac{8}{{15}}} \right) = \frac{4}{9}.\left( { - \frac{{15}}{8}} \right) = \frac{{ - 5}}{6}\)
h)\(\left( {1\frac{2}{3}} \right):\left( {2\frac{1}{2}} \right) = \frac{5}{3}:\frac{5}{2} = \frac{5}{3}.\frac{2}{5} = \frac{2}{3}\)
i) \(\frac{2}{5}.\left( { - 1,25} \right) = \frac{2}{5}.\frac{{ - 5}}{4} = \frac{{ - 1}}{2}\)
k) \(\left( {\frac{{ - 3}}{5}} \right).\left( {\frac{{15}}{{ - 7}}} \right).3\frac{1}{9} = \left( {\frac{{ - 3}}{5}} \right).\left( {\frac{{15}}{{ - 7}}} \right).\frac{{28}}{9} = \frac{{ - 3.3.5.7.4}}{{5.\left( { - 7} \right).3.3}} = 4\)
Bài 2 trang 15 sgk toán 7 tập 1 chân trời sáng tạo
Câu hỏi
Tính:
a)\(0,75 - \frac{5}{6} + 1\frac{1}{2};\)
b)\(\frac{3}{7} + \frac{4}{{15}} + \left( {\frac{{ - 8}}{{21}}} \right) + \left( { - 0,4} \right);\)
c)\(0,625 + \left( {\frac{{ - 2}}{7}} \right) + \frac{3}{8} + \left( {\frac{{ - 5}}{7}} \right) + 1\frac{2}{3}\)
d)\(\left( { - 3} \right).\left( {\frac{{ - 38}}{{21}}} \right).\left( {\frac{{ - 7}}{6}} \right).\left( { - \frac{3}{{19}}} \right);\)
e) \(\left( {\frac{{11}}{{18}}:\frac{{22}}{9}} \right).\frac{8}{5};\)
g)\(\left[ {\left( {\frac{{ - 4}}{5}} \right).\frac{5}{8}} \right]:\left( {\frac{{ - 25}}{{12}}} \right)\)
Bài giải
a)
\(\begin{array}{l}0,75 - \frac{5}{6} + 1\frac{1}{2} = \frac{3}{4} - \frac{5}{6} + \frac{3}{2}\\ = \frac{9}{{12}} - \frac{{10}}{{12}} + \frac{{18}}{{12}} = \frac{{17}}{{12}}\end{array}\)
b)
\(\begin{array}{l}\frac{3}{7} + \frac{4}{{15}} + \left( {\frac{{ - 8}}{{21}}} \right) + \left( { - 0,4} \right) = \frac{3}{7} + \frac{4}{{15}} - \frac{8}{{21}} - \frac{2}{5}\\ = \left( {\frac{3}{7} - \frac{8}{{21}}} \right) + \left( {\frac{4}{{15}} - \frac{2}{5}} \right)\\ = \left( {\frac{9}{{21}} - \frac{8}{{21}}} \right) + \left( {\frac{4}{{15}} - \frac{6}{{15}}} \right)\\ = \frac{1}{{21}} + \left( {\frac{{ - 2}}{{15}}} \right)\\ = \frac{5}{{105}} - \frac{{14}}{{105}}\\ = \frac{{ - 9}}{{105}} = \frac{{ - 3}}{{35}}\end{array}\)
c)
\(\begin{array}{l}0,625 + \left( {\frac{{ - 2}}{7}} \right) + \frac{3}{8} + \left( {\frac{{ - 5}}{7}} \right) + 1\frac{2}{3}\\ = \frac{5}{8} + \left( {\frac{{ - 2}}{7}} \right) + \frac{3}{8} - \frac{5}{7} + \frac{5}{3}\\ = \left( {\frac{5}{8} + \frac{3}{8}} \right) + \left( {\frac{{ - 2}}{7} - \frac{5}{7}} \right) + \frac{5}{3}\\ = 1 - 1 + \frac{5}{3} = \frac{5}{3}\end{array}\)
d)
\(\begin{array}{l}\left( { - 3} \right).\left( {\frac{{ - 38}}{{21}}} \right).\left( {\frac{{ - 7}}{6}} \right).\left( { - \frac{3}{{19}}} \right)\\ = \frac{{ - 3.\left( { - 38} \right).\left( { - 7} \right).\left( { - 3} \right)}}{{21.6.19}}\\ = \frac{{3.38.7.3}}{{21.6.19}}\\ = \frac{{3.2.19.7.3}}{{3.7.3.2.19}}\\ = 1\end{array}\)
e)
\(\begin{array}{l}\left( {\frac{{11}}{{18}}:\frac{{22}}{9}} \right).\frac{8}{5} = \left( {\frac{{11}}{{18}}.\frac{9}{{22}}} \right).\frac{8}{5}\\ = \frac{{11.9.4.2}}{{9.2.2.11.5}} = \frac{2}{5}\end{array}\)
g)
\(\left[ {\left( {\frac{{ - 4}}{5}} \right).\frac{5}{8}} \right]:\left( {\frac{{ - 25}}{{12}}} \right) = \frac{{ - 20}}{{40}}:\left( {\frac{{ - 25}}{{12}}} \right)\\ = \frac{{ - 1}}{2}.\frac{{ - 12}}{{25}} = \frac{6}{{25}}\)
Bài 3 trang 15 sgk toán 7 tập 1 chân trời sáng tạo
Câu hỏi
Thay dấu ? bằng dấu (>,<,=) thích hợp.
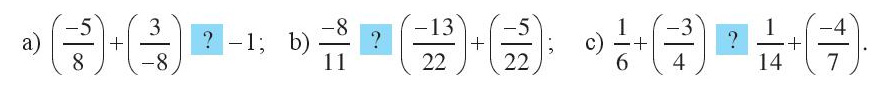
Bài giải
a)\(\left( {\frac{{ - 5}}{8}} \right) + \left( {\frac{3}{{ - 8}}} \right) = \left( {\frac{{ - 5}}{8}} \right) + \left( {\frac{{ - 3}}{8}} \right) = - 1\)
Vậy dấu cần điền là “=”.
b)\(\left( {\frac{{ - 13}}{{22}}} \right) + \left( {\frac{{ - 5}}{{22}}} \right) = \frac{{ - 18}}{{22}} = \frac{{ - 9}}{{11}} < \frac{{ - 8}}{{11}}\).
Vậy dấu cần điền là “>”.
c) \(\frac{1}{6} + \left( {\frac{{ - 3}}{4}} \right) = \frac{2}{{12}} + \left( {\frac{{ - 9}}{{12}}} \right) = \frac{{ - 7}}{{12}}\)
\(\frac{1}{{14}} + \left( {\frac{{ - 4}}{7}} \right) = \frac{1}{{14}} + \left( {\frac{{ - 8}}{{14}}} \right) = \frac{{ - 7}}{{14}}\)
Mà \(\frac{{ - 7}}{{12}} < \frac{{ - 7}}{{14}}\)
Vậy dấu cần điền là “<”.
Bài 4 trang 15 sgk toán 7 tập 1 chân trời sáng tạo
Câu hỏi
Tính:
a)\(\frac{3}{7}.\left( { - \frac{1}{9}} \right) + \frac{3}{7}.\left( { - \frac{2}{3}} \right);\)
b)\(\left( {\frac{{ - 7}}{{13}}} \right).\frac{5}{{12}} + \left( {\frac{{ - 7}}{{13}}} \right).\frac{7}{{12}} + \left( {\frac{{ - 6}}{{13}}} \right);\)
c)\(\left[ {\left( {\frac{{ - 2}}{3} + \frac{3}{7}} \right)} \right]:\frac{5}{9} + \left( {\frac{4}{7} - \frac{1}{3}} \right):\frac{5}{9}\)
d)\(\frac{5}{9}:\left( {\frac{1}{{11}} - \frac{5}{{22}}} \right) + \frac{5}{9}:\left( {\frac{1}{{15}} - \frac{2}{3}} \right);\)
e) \(\frac{3}{5} + \frac{3}{{11}} - \left( {\frac{{ - 3}}{7}} \right) + \left( {\frac{{ - 2}}{{97}}} \right) - \frac{1}{{35}} - \frac{3}{4} + \left( {\frac{{ - 23}}{{44}}} \right)\)
Bài giải
a)
\(\begin{array}{l}\frac{3}{7}.\left( { - \frac{1}{9}} \right) + \frac{3}{7}.\left( { - \frac{2}{3}} \right)\\ = \frac{3}{7}.\left( { - \frac{1}{9} + \frac{-2}{3}} \right)\\ = \frac{3}{7}.\left( { - \frac{1}{9} - \frac{6}{9}} \right)\\ = \frac{3}{7}.\frac{{ - 7}}{9} = \frac{{ - 1}}{3}\end{array}\)
b)
\(\begin{array}{l}\left( {\frac{{ - 7}}{{13}}} \right).\frac{5}{{12}} + \left( {\frac{{ - 7}}{{13}}} \right).\frac{7}{{12}} + \left( {\frac{{ - 6}}{{13}}} \right)\\ = \frac{{ - 7}}{{13}}.\left( {\frac{5}{{12}} + \frac{7}{{12}}} \right) + \left( {\frac{{ - 6}}{{13}}} \right)\\ = \frac{{ - 7}}{{13}}.1 + \left( {\frac{{ - 6}}{{13}}} \right)\\ = \frac{{ - 7}}{{13}} + \left( {\frac{{ - 6}}{{13}}} \right)\\ = \frac{{ - 13}}{{13}}\\ = -1\end{array}\)
c)
\(\begin{array}{l}\left[ {\left( {\frac{{ - 2}}{3} + \frac{3}{7}} \right)} \right]:\frac{5}{9} + \left( {\frac{4}{7} - \frac{1}{3}} \right):\frac{5}{9}\\ = \left[ {\left( {\frac{{ - 2}}{3} + \frac{3}{7}} \right)} \right].\frac{9}{5} + \left( {\frac{4}{7} - \frac{1}{3}} \right).\frac{9}{5}\\ = \left( {\frac{{ - 2}}{3} + \frac{3}{7} + \frac{4}{7} - \frac{1}{3}} \right).\frac{9}{5}\\ = \left[ {\left( {\frac{{ - 2}}{3} - \frac{1}{3}} \right) + \left( {\frac{3}{7} + \frac{4}{7}} \right)} \right].\frac{9}{5}\\ = \left( { - 1 + 1} \right).\frac{9}{5}\\ = 0.\frac{9}{5} = 0\end{array}\)
d)
\(\begin{array}{l}\frac{5}{9}:\left( {\frac{1}{{11}} - \frac{5}{{22}}} \right) + \frac{5}{9}:\left( {\frac{1}{{15}} - \frac{2}{3}} \right)\\ = \frac{5}{9}:\left( {\frac{2}{{22}} - \frac{5}{{22}}} \right) + \frac{5}{9}:\left( {\frac{1}{{15}} - \frac{{10}}{{15}}} \right)\\ = \frac{5}{9}:\frac{{ - 3}}{{22}} + \frac{5}{9}:\frac{{ - 9}}{15}\\= \frac{5}{9}:\frac{{ - 3}}{{22}} + \frac{5}{9}:\frac{{ - 3}}{5}\\ = \frac{5}{9}.\frac{{ - 22}}{3} + \frac{5}{9}.\frac{{ - 5}}{3}\\ = \frac{5}{9}.\left( {\frac{{ - 22}}{3} - \frac{5}{3}} \right)\\ = \frac{5}{9}.\frac{-27}{3}= \frac{5}{9}.\left( { - 9} \right) = - 5\end{array}\)
e)
\(\begin{array}{l}\frac{3}{5} + \frac{3}{{11}} - \left( {\frac{{ - 3}}{7}} \right) + \left( {\frac{{ - 2}}{{97}}} \right) - \frac{1}{{35}} - \frac{3}{4} + \left( {\frac{{ - 23}}{{44}}} \right)\\ = \frac{3}{5} + \frac{3}{{11}} + \frac{3}{7} - \frac{2}{{97}} - \frac{1}{{35}} - \frac{3}{4} - \frac{{23}}{{44}}\\ = \left( {\frac{3}{5} + \frac{3}{7} - \frac{1}{{35}}} \right) + \left( {\frac{3}{{11}} - \frac{3}{4} - \frac{{23}}{{44}}} \right) - \frac{2}{{97}}\\ = \left( {\frac{{21}}{{35}} + \frac{{15}}{{35}} - \frac{1}{{35}}} \right) + \left( {\frac{{12}}{{44}} - \frac{{33}}{{44}} - \frac{{23}}{{44}}} \right) - \frac{2}{{97}}\\ = 1 + \left( { - 1} \right) - \frac{2}{{97}}\\ = - \frac{2}{{97}}\end{array}\)
Bài 5 trang 15 sgk toán 7 tập 1 chân trời sáng tạo
Câu hỏi
Tìm x, biết:
a)\(x.\frac{{14}}{{27}} = \frac{{ - 7}}{9}\)
b)\(\left( {\frac{{ - 5}}{9}} \right):x = \frac{2}{3};\)
c)\(\frac{2}{5}:x = \frac{1}{{16}}:0,125\)
d)\( - \frac{5}{{12}}x = \frac{2}{3} - \frac{1}{2}\)
Bài giải
a)
\(\begin{array}{l}x.\frac{{14}}{{27}} = \frac{{ - 7}}{9}\\x = \frac{{ - 7}}{9}:\frac{{14}}{{27}}\\x = \frac{{ - 7}}{9}.\frac{{27}}{{14}}\\x = \frac{{ - 3}}{2}\end{array}\)
Vậy \(x = \frac{{ - 3}}{2}\).
b)
\(\begin{array}{l}\left( {\frac{{ - 5}}{9}} \right):x = \frac{2}{3}\\x = \left( {\frac{{ - 5}}{9}} \right):\frac{2}{3}\\x = \left( {\frac{{ - 5}}{9}} \right).\frac{3}{2}\\x = \frac{{ - 5}}{6}\end{array}\)
Vậy \(x = \frac{{ - 5}}{6}\).
c)
\(\begin{array}{l}\frac{2}{5}:x = \frac{1}{{16}}:0,125\\\frac{2}{5}:x = \frac{1}{{16}}:\frac{1}{8}\\\frac{2}{5}:x = \frac{1}{{16}}.8\\\frac{2}{5}:x = \frac{1}{2}\\x = \frac{2}{5}:\frac{1}{2}\\x = \frac{2}{5}.2\\x = \frac{4}{5}\end{array}\)
Vậy \(x = \frac{4}{5}\)
d)
\(\begin{array}{l} - \frac{5}{{12}}x = \frac{2}{3} - \frac{1}{2}\\ - \frac{5}{{12}}x = \frac{4}{6} - \frac{3}{6}\\ - \frac{5}{{12}}x = \frac{1}{6}\\x = \frac{1}{6}:\left( { - \frac{5}{{12}}} \right)\\x = \frac{1}{6}.\frac{{ - 12}}{5}\\x = \frac{{ - 2}}{5}\end{array}\)
Vậy \(x = \frac{{ - 2}}{5}\).
Chú ý: Khi trình bày lời giải bài tìm x, sau khi tính xong, ta phải kết luận.
Bài tiếp theo: Trang 16 SGK Toán 7 tập 1 Chân trời sáng tạo
Xem thêm:
- Trang 9 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 10 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 20 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 21 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 25 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 27 SGK Toán 7 tập 1 Chân trời sáng tạo
- Trang 28 SGK Toán 7 tập 1 Chân trời sáng tạo
Trên đây là chi tiết hướng dẫn Giải bài tập Trang 15 SGK Toán 7 tập 1 Chân trời sáng tạo được Đọc Tài Liệu biên soạn với mong muốn hỗ trợ các em học sinh học tốt hơn môn Toán lớp 7
Hướng dẫn giải Toán 7 Chân trời sáng tạo bởi Đọc Tài Liệu