Bài 4.16 trang 74 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
Cho hai tam giác ABC và DEF thoả mãn \(AB = DE,AC = DF,\widehat {BAC} = \widehat {EDF} = {60^\circ },BC = 6\;{\rm{cm}},\widehat {ABC} = {45^\circ }\). Tính độ dài cạnh EF và số đo các góc ACB, DEF, EFD.
Bài giải
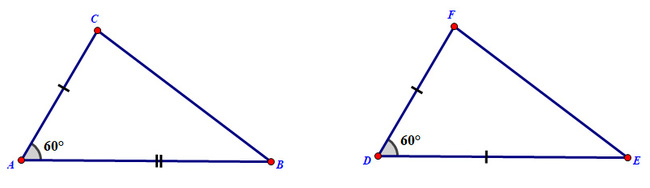
Xét hai tam giác ABC và DEF có:
\(\begin{array}{l}AB = DE\\AC = DF\\\widehat {BAC} = \widehat {EDF} = {60^\circ }\end{array}\)
\(\Rightarrow \Delta ABC = \Delta DEF\)(c.g.c)
Do đó:
\(EF = BC = 6cm\)
\(\widehat {DEF} = \widehat {ABC} = {45^o}\)
\(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^o}\\ \Rightarrow {60^o} + {45^o} + \widehat {ACB} = {180^o}\\ \Rightarrow \widehat {ACB} = {75^o}\end{array}\)
\( \Rightarrow \widehat {EFD} = \widehat {ACB} = {75^o}\)
Bài 4.17 trang 74 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
Cho hai tam giác ABC và DEF thoả mãn \(AB = DE\), \(\widehat {ABC} = \widehat {DEF} = {70^\circ },\widehat {BAC} = \widehat {EDF} = {60^\circ },AC = 6\;{\rm{cm}}.\)
Tính độ dài cạnh DF.
Bài giải
Xét hai tam giác ABC và DEF có:
\(\begin{array}{l}\widehat {ABC} = \widehat {DEF} (= {70^\circ })\\AB = DE\\\widehat {BAC} = \widehat {EDF} (= {60^\circ })\end{array}\)
\( \Rightarrow \Delta ABC{\rm{ = }}\Delta DEF\)
(g.c.g)\( \Rightarrow DF = AC\)( 2 cạnh tương ứng)
Mà AC = 6 cm
\( \Rightarrow DF = 6cm\)
Bài 4.18 trang 74 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
Cho Hình 4.44, biết \(EC = ED\) và \(\widehat {AEC} = \widehat {AED}\). Chứng minh rằng:
\(\begin{array}{*{20}{l}}{{\rm{ a) }}\Delta AEC = \Delta AED;}&{{\rm{ b) }}\Delta ABC = \Delta ABD.}\end{array}\)
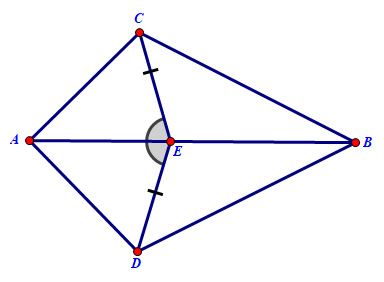
Bài giải
a)Xét hai tam giác AEC và AED có
\(EC = ED\)
\(\widehat {CEA} = \widehat {DEA}\)
AE chung
\( \Rightarrow \Delta AEC{\rm{ = }}\Delta AED\)(c.g.c)
b)
Do \(\Delta AEC{\rm{ = }}\Delta AED\) nên \(\widehat {CAE} = \widehat {DAE}\) ( 2 góc tương ứng) và AC=AD ( 2 cạnh tương ứng).
Xét \(\Delta ABC\) và \(\Delta ABD\) có:
AB chung
\(\widehat {CAE} = \widehat {DAE}\)
AC=AD
\( \Rightarrow \Delta ABC = \Delta ABD\)(c.g.c)
Bài 4.19 trang 74 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A,B,C lần lượt thuộc các tia Ox, Oy, Oz sao cho \(\widehat {CAO} = \widehat {CBO}.\)
a) Chứng minh rằng \(\Delta OAC = \Delta OBC\).
b) Lấy điểm \(M\) trên tia đối của tia CO. Chứng minh rằng \(\Delta MAC = \Delta MBC\).
Bài giải
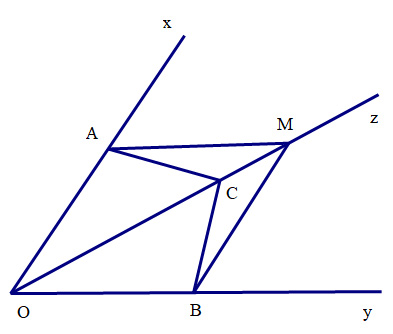
a)
Xét \(\Delta OAC\) và \(\Delta OBC\) có:
\(\widehat {AOC} = \widehat {AOB}\)(Oz là phân giác góc xOy)
OC chung
\(\widehat {CAO} = \widehat {CBO}.\)
\(\Rightarrow \Delta OAC = \Delta OBC\)(g.c.g)
b) Do \(\Delta OAC = \Delta OBC\) nên AC=BC ( 2 cạnh tương ứng)
Vì \(\widehat {ACO}\) và \(\widehat {ACM}\) kề bù
\(\widehat {BCO}\) và \(\widehat {BCM}\) kề bù
Mà \(\widehat {ACO} = \widehat {BCO}\) nên \(\widehat {ACM} = \widehat {BCM}\)
Xét \(\Delta MAC\) và \(\Delta MBC\) có:
AC=BC
\(\widehat {ACM} = \widehat {BCM}\)
CM chung
\( \Rightarrow \Delta MAC = \Delta MBC\)(c.g.c)
Bài tiếp theo: Trang 79 SGK Toán 7 tập 1 Kết nối tri thức
Xem thêm:
- Trang 62 SGK Toán 7 tập 1 Kết nối tri thức
- Trang 67 SGK Toán 7 tập 1 Kết nối tri thức
- Trang 69 SGK Toán 7 tập 1 Kết nối tri thức
- Trang 73 SGK Toán 7 tập 1 Kết nối tri thức
- Trang 84 SGK Toán 7 tập 1 Kết nối tri thức
- Trang 86 SGK Toán 7 tập 1 Kết nối tri thức
- Trang 87 SGK Toán 7 tập 1 Kết nối tri thức
Trên đây là chi tiết hướng dẫn Giải bài tập Trang 74 SGK Toán 7 tập 1 Kết nối tri thức được Đọc Tài Liệu biên soạn với mong muốn hỗ trợ các em học sinh học tốt hơn môn Toán lớp 7
Hướng dẫn giải Toán 7 Kết nối tri thức bởi Đọc Tài Liệu