Bài 4.12 trang 73 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
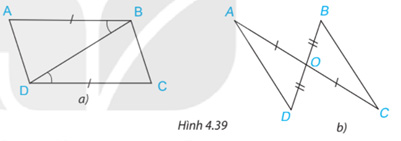
Trong mỗi hình bên (H.4.39), hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.
Bài giải
a)Xét tam giác ABD và tam giác CBD có:
AB=CD
\(\widehat {ABD} = \widehat {CDB}\)
BD chung
Vậy \(\Delta ABD = \Delta CBD\)(c.g.c)
b)Xét hai tam giác OAD và OCB có:
AO=CO
\(\widehat {AOD} = \widehat {COB}\)(đối đỉnh)
OD=OB
Vậy \(\Delta OAD = \Delta OCB\)(c.g.c)
Bài 4.13 trang 73 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như Hình 4.40.
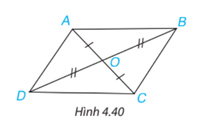
a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau;
b) Chứng minh rằng \(\Delta \)DAB = \(\Delta \)BCD.
Bài giải
a) Xét tam giác AOB và COD, có:
AO = CO
\(\widehat{AOB}=\widehat{COD}\) ( đối đỉnh)
OB = OD
\(\Rightarrow \Delta AOB = \Delta COD\) ( c.g.c)
Xét tam giác AOD và COB, có:
AO = CO
\(\widehat{AOD}=\widehat{COB}\) ( đối đỉnh)
OD = OB
\(\Rightarrow \Delta AOD = \Delta COB\) ( c.g.c)
Vậy hai cặp tam giác có chung đỉnh O bằng nhau là: AOB và COD; AOD và COB theo trường hợp cạnh – góc – cạnh.
b)
Do hai tam giác AOD và COB nên: \(\widehat {ADO} = \widehat {CBO}\) (2 góc tương ứng) và AD=BC (2 cạnh tương ứng)
Xét \(\Delta \)DAB và \(\Delta \)BCD có:
AD=BC
\(\widehat {ADO} = \widehat {CBO}\)
BD chung
Vậy \(\Delta \)DAB =\(\Delta \)BCD (c.g.c)
Bài 4.14 trang 73 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
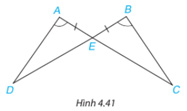
Chứng minh rằng hai tam giác ADE và BCE trong Hình 4.41 bằng nhau.
Bài giải
Xét hai tam giác ADE và BCE có:
\(\widehat A = \widehat B\)
AE=BE
\(\widehat {AED} = \widehat {BEC}\)(đối đỉnh)
Vậy \(\Delta ADE = \Delta BCE\)(g.c.g)
Bài 4.15 trang 73 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như Hình 4.42. Gọi E là giao điểm của hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G, E, H thẳng hàng. Chứng minh rằng:
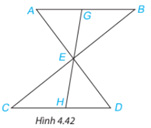
a) \(\Delta \)ABE =\(\Delta \)DCE;
b) EG = EH.
Bài giải
a)Xét hai tam giác ABE và DCE có:
\(\widehat {BAE} = \widehat {CDE}\)(so le trong)
AB=CD(gt)
\(\widehat {ABE} = \widehat {DCE}\)(so le trong)
Vậy \(\Delta \)ABE =\(\Delta \)DCE(g.c.g)
b)Xét hai tam giác BEG và CEH có:
\(\widehat {CEH} = \widehat {BEG}\)(đối đỉnh)
CE=BE (do \(\Delta \)ABE =\(\Delta \)DCE)
\(\widehat {ECH} = \widehat {EBG}\)(so le trong)
Suy ra \(\Delta BEG{\rm{ = }}\Delta CEH\)(g.c.g)
Vậy EG=EH (hai cạnh tương ứng).
Bài tiếp theo: Trang 74 SGK Toán 7 tập 1 Kết nối tri thức
Xem thêm:
- Trang 62 SGK Toán 7 tập 1 Kết nối tri thức
- Trang 67 SGK Toán 7 tập 1 Kết nối tri thức
- Trang 69 SGK Toán 7 tập 1 Kết nối tri thức
- Trang 79 SGK Toán 7 tập 1 Kết nối tri thức
- Trang 84 SGK Toán 7 tập 1 Kết nối tri thức
- Trang 86 SGK Toán 7 tập 1 Kết nối tri thức
- Trang 87 SGK Toán 7 tập 1 Kết nối tri thức
Trên đây là chi tiết hướng dẫn Giải bài tập Trang 73 SGK Toán 7 tập 1 Kết nối tri thức được Đọc Tài Liệu biên soạn với mong muốn hỗ trợ các em học sinh học tốt hơn môn Toán lớp 7
Hướng dẫn giải Toán 7 Kết nối tri thức bởi Đọc Tài Liệu