Tìm các hằng số a và b sao cho (x3 + ax + b) : (x + 1) dư 7 và (x3 + ax + b) : (x-3) dư 5

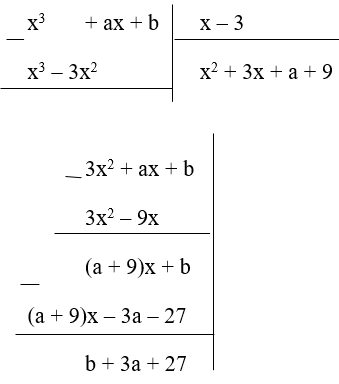
Để ${x}^3$ + ax + b chia cho x + 1 dư 7 thì b - a - 1 = 7
$\Leftrightarrow$ -a + b = 8 (1)
Để ${x}^3$ + ax + b chia cho x - 3 dư -5 thì b + 3a + 27 = -5
$\Leftrightarrow$ 3a + b = -32 (2)
Từ (1) và (2) ta có hệ $\left\{ \matrix{-{a}+{b}={8}\hfill \cr{3}{a}+{b}=-{32}\hfill \cr} \right.$
$\Leftrightarrow$ $\left\{ \matrix{{a}=-{10}\hfill \cr{b}=-{2}\hfill \cr} \right.$
Vậy a = -10, b = -2
Đáp án cần chọn là: C