Gọi a là cạnh của khối lập phương. Áp dụng định luật khúc xạ ở mặt trên ta có: sini = n.sinr (1)
Điều kiện góc tới ${i}={i}_{{m}{a}{x}}$ để tia khúc xạ vào trong khối còn gặp mặt đáp của khối là tia khúc xạ trùng với phương IJ với J là đỉnh của hình hộp như hình vẽ: ${r}={r}_{{m}{a}_x}$
Trong đó: $IH= a; HJ=\dfrac{a\sqrt{2}}{2} \rightarrow IJ=\sqrt{IH^2 +HJ^2}=\sqrt{{a}^{2}+\left(\frac{\mathrm{a} \sqrt{2}}{2}\right)^{2}}=a.\sqrt{\dfrac{3}{2}}$
Do đó:
$ \sin r_{\max }=\dfrac{H J}{I J}=\frac{\frac{a}{\sqrt{2}}}{a \cdot\sqrt{\frac{3}{2}}}=\frac{1}{\sqrt{3}}$
Từ (1) và (2) suy ra
$sini_{max }=1,5\cdot \dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{2} \rightarrow i_{max }=60$
Một tia sáng được chiếu điến giữa của mặt trên của khối lập phương trong suốt,
Xuất bản: 12/01/2021 - Cập nhật: 26/10/2023 - Tác giả: Chu Huyền
Câu Hỏi:
Một tia sáng được chiếu điến giữa của mặt trên của khối lập phương trong suốt, chiết suất n = 1,50 (hình vẽ). Tìm góc tới i lớn nhất để tia khúc xạ vào trong khối còn gặp mặt đáy của khối.
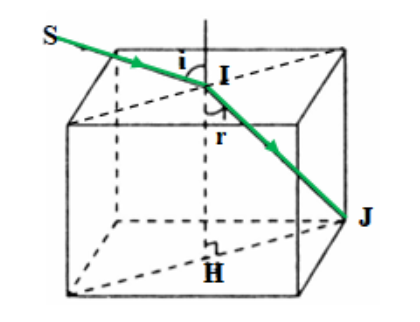

Câu hỏi trong đề: Trắc nghiệm Vật lý 11 bài 26: Khúc xạ ánh sáng
Đáp án và lời giải
đáp án đúng: B
