Lý thuyết định lí đảo và hệ quả của định lí Ta-let và các dạng bài thường gặp

Nếu đang tìm kiếm một tài liệu học tập về phần định lí Ta-let, các em hãy tham khảo ngay tài liệu dưới đây với hệ thống lý thuyết định lí đảo và hệ quả của định lí Ta-let cùng các dạng bài tập thường gặp, giúp các em nắm được trọn vẹn phần kiến thức này. Các thầy cô cũng có thể sử dụng bài tổng hợp này như một tài liệu hữu ích phục vụ quá trình dạy học của mình.

Cùng tham khảo nhé!

I. Lý thuyết định lí đảo và hệ quả của định lí Ta-let

1. Định lí Ta-lét đảo

Ví dụ:\(\Delta ABC\) có  \(\dfrac{{AD}}{{DB}} = \dfrac{{AE}}{{EC}} \Rightarrow DE{\rm{//}}BC\)

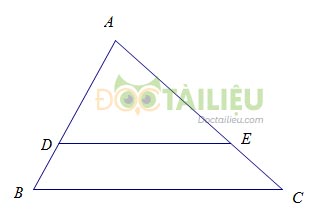
2. Hệ quả của định lí Ta-lét

\(\Delta ABC,DE//BC \Rightarrow \dfrac{{AD}}{{AB}}= \dfrac{{AE}}{{AC}} = \dfrac{{DE}}{{BC}}\)

Chú ý: Hệ quả trên vẫn đúng cho trường hợp đường thẳng \(a\) song song với một cạnh của tam giác và cắt phần kéo dài của hai cạnh còn lại.

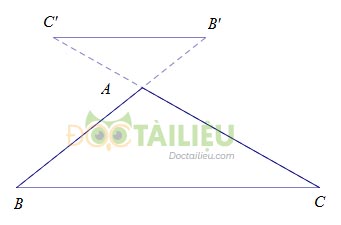
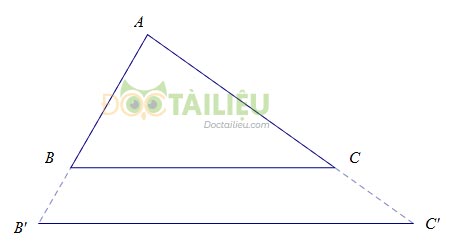
Ở hai hình trên \(\Delta ABC\) có \(BC{\rm{//}}B'C'\Rightarrow \dfrac{{AB'}}{{AB}} = \dfrac{{AC'}}{{AC}} = \dfrac{{B'C'}}{{BC}}.\)

II. Các dạng toán thường gặp về định lí đảo và hệ quả của định lí Ta-let

Dạng 1: Tính độ dài đoạn thẳng, chu vi, diện tích và các tỉ số.

Phương pháp:

Sử dụng định lí Ta-lét, hệ quả định lí Ta-lét, tỉ số đoạn thẳng để tính toán.

+ Định lý: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

+ Hệ quả: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh tam giác đã cho.

+ Ngoài ra, ta còn sử dụng đến tính chất tỉ lệ thức:

Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\) thì \( \left\{ \begin{array}{l}ad = bc\\\dfrac{a}{c} = \dfrac{b}{d}\\\dfrac{{a + b}}{b} = \dfrac{{c + d}}{d};\,\dfrac{{a - b}}{b} = \dfrac{{c - d}}{d}\\\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{a + c}}{{b + d}} = \dfrac{{a - c}}{{b - d}}\end{array} \right.\)

Dạng 2: Chứng minh hai đường thẳng song song, chứng minh các đẳng thức hình học.

Phương pháp:

Ta sử dụng định lí Ta-lét, định lí đảo và hệ quả để chứng minh.

III. Bài tập mẫu về định lí đảo và hệ quả của định lí Ta-let

Cho tam giác \(ABC\) có cạnh \(BC = a.\) Trên cạnh \(AB\) lấy các điểm \(D\) và \(E\) sao cho \(AD = DE = EB.\) Từ \(D, E\) kẻ các đường thẳng song song với \(BC\), cắt cạnh \(AC\) theo thứ tự tại \(M, N\)

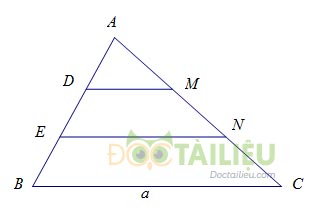
Tính theo \(a\) độ dài của các đoạn thẳng \(DM\) và \(EN\)

Lời giải chi tiết

Ta có: \(\displaystyle AD = DE = EB = {1 \over 3}AB\) (1)

Suy ra: \(\displaystyle AE = AD + DE = {2 \over 3}AB\)        (2)

Xét \(∆ ABC\) có \(DM // BC\) (gt)

Theo hệ quả định lí Ta-lét ta có:\(\displaystyle {{AD} \over {AB}} = {{DM} \over {BC}} \displaystyle \Rightarrow {{AD} \over {AB}} = {{DM} \over a} (3)\)

Từ (1) và (3) ta có: \(\displaystyle {{DM} \over a} = {1 \over 3}\)

\(\displaystyle \Rightarrow DM = {1 \over 3}a\)

Xét \(∆ ABC\) có \(EN // BC\) (gt)

Theo hệ quả định lí Ta-lét ta có:\(\displaystyle {{AE} \over {AB}} = {{EN} \over {BC}}\displaystyle \Rightarrow {{AE} \over {AB}} = {{EN} \over a}        (4)\)

Từ (2) và (4) ta có: \(\displaystyle {{EN} \over a} = {2 \over 3}\)

\(\displaystyle\Rightarrow EN = {2 \over 3}a\)

********************

Trên đây là tổng hợp lý thuyết định lí đảo và hệ quả của định lí Ta-let và các dạng bài thường gặp bao gồm các kiến thức cần nắm và cách làm các dạng bài tập liên quan mà Đọc tài liệu đã tổng hợp. Hy vọng đây sẽ là tài liệu học tập hữu ích cho các em học sinh cũng như các phụ huynh trong quá trình dạy học cho con em mình tại nhà. Ngoài ra đừng quên xem thêm những kiến thức khác và cách giải Toán 8 được cập nhật liên tục tại doctailieu.com. Chúc các em luôn học tốt và đạt kết quả cao!