Hệ thống kiến thức lý thuyết Hình thang cân và tổng hợp các dạng toán thường gặp cùng hướng dẫn chi tiết cách làm, qua đó giúp các em nắm được kiến thức từ khái quát đến chi tiết để học tốt phần kiến thức này.
Mời các em cùng tham khảo:

I. Lý thuyết Hình thang cân
Hình thang cân
Định nghĩa: Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
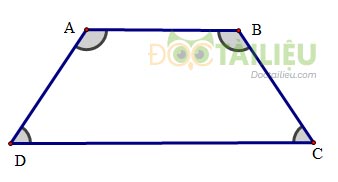
Tính chất:
Định lí 1: Trong một hình thang cân, hai cạnh bên bằng nhau.
\(ABCD\) là hình thang cân (đáy \(AB, CD\)) \( \Rightarrow AD = BC\)
Định lí 2: Trong một hình thang cân, hai đường chéo bằng nhau.
\(ABCD\) là hình thang cân (đáy \(AB, CD\)) \( \Rightarrow AC = BD\)
Định lí 3: Hình thang có hai đường chéo bằng nhau là hình thang cân.
Hình thang \(ABCD\) (đáy \(AB, CD\)) có \(AC = BD\) \( \Rightarrow ABCD\) là hình thang cân.
Dấu hiệu nhận biết:
+ Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
+ Hình thang có hai đường chéo bằng nhau là hình thang cân.
Ví dụ:
+ \(ABCD\) là hình thang cân thì \(AD = BC;\,AC = BD\)
+ Tứ giác \(ABCD\) có \(\left\{ \begin{array}{l}AB{\rm{//}}CD\\\widehat D = \widehat C\end{array} \right. \Leftrightarrow ABCD\) là hình thang cân.
+ Tứ giác \(ABCD\) có \( \left\{ \begin{array}{l}AB{\rm{//}}CD\\\widehat A = \widehat B\end{array} \right. \Leftrightarrow ABCD\) là hình thang cân.
+ Tứ giác \(ABCD\) có \(\left\{ \begin{array}{l}AB{\rm{//}}CD\\AC = BD\end{array} \right. \Leftrightarrow ABCD\) là hình thang cân.
II. Một số dạng bài thường gặp
Dạng 1: Chứng minh và tính các góc của hình thang cân dựa vào tính chất hình.
Phương pháp:
Ta sử dụng các kiến thức:
+ Tính chất của hình thang cân (ở trên)
+ Tổng bốn góc của một tứ giác bằng \(360^\circ\) .
+ Góc ngoài của tứ giác là góc kề bù với một góc của tứ giác.
+ Hai góc kề một cạnh bên của hình thang bằng \({180^0}\) .
Dạng 2: Chứng minh một tứ giác là hình thang cân
Phương pháp:
Ta sử dụng định nghĩa và các dấu hiệu nhận biết để chứng minh.
*******************
Hy vọng với hệ thống kiến thức lý thuyết Hình thang cân trên đây, các em sẽ có thêm một tài liệu học tập hữu ích để học tốt hơn môn Toán 8. Chúc các em luôn học tốt và đạt kết quả cao!