Bạn đang tìm kiếm tài liệu tổng hợp kiến thức về hình thang? Hãy tham khảo ngay bài viết dưới đây của Đọc tài liệu với những lý thuyết về hình thang cùng tổng hợp các dạng toán cơ bản thường gặp. Đây sẽ là tài liệu học tập hữu ích cho học sinh và đồng thời giúp các thầy cô có thêm tài liệu hay phục vụ việc dạy học.
Cùng tham khảo nhé!

I. Lý thuyết hình thang
Hình thang
Định nghĩa: Hình thang là tứ giác có hai cạnh đối song song.
Hai góc kề một cạnh bên của hình thang có tổng bằng {180^0}
Nhận xét:
+ Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.
+ Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau.
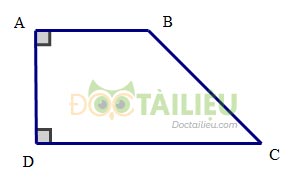
+ Hình thang vuông là hình thang có một góc vuông.
Ví dụ 1:
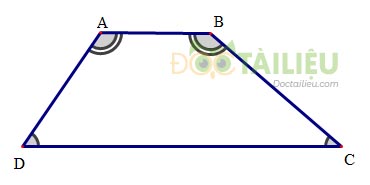
\(ABCD\) là hình thang. Khi đó:
+ \(AB{\rm{//}}CD\), \(AB,CD\) là hai đáy, \(AD,BC\) là cạnh bên.
+ \(\widehat A + \widehat D = \widehat B + \widehat C = 180^\circ \)
+ Nếu \(AD{\rm{//}}BC \Leftrightarrow \left\{ \begin{array}{l}AD = BC\\AB = CD\end{array} \right.\)
+ Nếu \(AB = CD \Leftrightarrow \left\{ \begin{array}{l}AD = BC\\AD{\rm{//}}BC\end{array} \right.\)
Hình thang cân
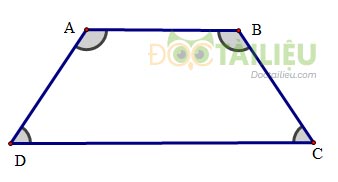
Tính chất:
+ Trong hình thang cân, hai cạnh bên bằng nhau.
+ Trong hình thang cân, hai đường chéo bằng nhau.
Dấu hiệu nhận biết:
+ Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
+ Hình thang có hai đường chéo bằng nhau là hình thang cân.
Ví dụ:
+ \(ABCD\) là hình thang cân thì \(AD = BC;\,AC = BD\)
+ Tứ giác \(ABCD\) có \(\left\{ \begin{array}{l}AB{\rm{//}}CD\\\widehat D = \widehat C\end{array} \right. \Leftrightarrow ABCD\) là hình thang cân.
+ Tứ giác \(ABCD\) có \( \left\{ \begin{array}{l}AB{\rm{//}}CD\\\widehat A = \widehat B\end{array} \right. \Leftrightarrow ABCD\) là hình thang cân.
+ Tứ giác \(ABCD\) có \(\left\{ \begin{array}{l}AB{\rm{//}}CD\\AC = BD\end{array} \right. \Leftrightarrow ABCD\) là hình thang cân.
2. Các dạng toán thường gặp
Dạng 1: Chứng minh và tính các góc của hình thang, hình thang vuông hình thang cân dựa vào tính chất hình.
Phương pháp:
Ta sử dụng các kiến thức:
+ Tính chất của hình thang, hình thang vuông, hình thang cân (ở trên)
+ Tổng bốn góc của một tứ giác bằng \(360^\circ\) .
+ Góc ngoài của tứ giác là góc kề bù với một góc của tứ giác.
+ Hai góc kề một cạnh bên của hình thang bằng \({180^0}\) .
Dạng 2: Chứng minh một tứ giác là hình thang, hình thang vuông, hình thang cân
Phương pháp:
Ta sử dụng định nghĩa và các dấu hiệu nhận biết để chứng minh.
*******************
Trên đây là lý thuyết Hình thang bao gồm các kiến thức cần nắm và những dạng bài liên quan. Hy vọng đây sẽ là tài liệu hữu ích phục vụ việc học tập của các em. Ngoài ra, các em hãy truy cập doctailieu.com để tham khảo thêm nhiều tài liệu học Toán lớp 8 phong phú khác mà chúng tôi đã sưu tầm và tổng hợp nhé. Chúc các em luôn học tốt và đạt kết quả cao!