Mời các em tham khảo tổng hợp lý thuyết Tứ giác bao gồm định nghĩa, các dạng tứ giác đặt biệt,..., kèm theo đó là một số dạng bài thường gặp cùng hướng dẫn cách làm, qua đó nắm được toàn bộ phần kiến thức về Tứ giác.
Cùng xem nhé!

I. Lý thuyết Tứ giác
Tứ giác
Tứ giác lồi
Ví dụ: Tứ giác \(ABCD\) là tứ giác lồi

Tổng các góc của một tứ giác
Ví dụ: Tứ giác \(ABCD\) có \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
Chú ý: Góc ngoài của tứ giác là góc kề bù với một góc của tứ giác.
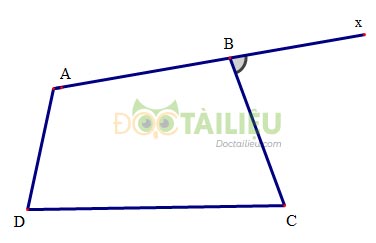
Ví dụ: Góc \(CBx\) là góc ngoài tại đỉnh \(B\) của tứ giác \(ABCD\ \Rightarrow \widehat {CBx} + \widehat {ABC} = 180^\circ .\)
Đa giác đều
2. Các dạng toán thường gặp
Dạng 1: Sử dụng tính chất về các góc của một tứ giác để tính góc
Phương pháp:
Ta sử dụng các kiến thức:
+ Tổng bốn góc của một tứ giác bằng \({360^0}\)
+ Góc ngoài của tứ giác là góc kề bù với một góc của tứ giác.
Dạng 2: Sử dụng bất đẳng thức tam giác để giải các bài toán liên quan đến các cạnh của một tứ giác
Phương pháp:
Ta sử dụng các kiến thức sau:
+ Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.
+ Trong một tam giác, hiệu độ dài hai cạnh bất kì bao giờ cũng nhỏ hơn độ dài cạnh còn lại.
+ Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng các độ dài của hai cạnh còn lại.
Nghĩa là: Trong tam giác \(ABC\) ta có \(\left| {AB-AC} \right| < BC < AB + AC.\)
***********************
Trên đây là tổng hợp lý thuyết Tứ giác và các dạng bài thường gặp bao gồm các kiến thức cần nắm và cách làm các dạng bài tập liên quan mà Đọc tài liệu đã tổng hợp. Hy vọng đây sẽ là tài liệu học tập hữu ích cho các em học sinh cũng như các phụ huynh trong quá trình dạy học cho con em mình tại nhà. Ngoài ra đừng quên xem thêm những kiến thức khác và cách giải Toán 8 được cập nhật liên tục tại doctailieu.com. Chúc các em luôn học tốt và đạt kết quả cao!