Bài 2 trang 66 SGK Toán 8 tập 1

Bạn tìm tài liệu hướng dẫn giải bài 6 trang 66 SGK Toán 8 tập 1? không cần tìm nữa...

Những nội dung dưới đây không chỉ giúp bạn biết được cách làm, tham khảo đáp án... mà còn hỗ trợ bạn ôn tập để nắm vững các kiến thức Toán 8 chương 1 phần hình học về tứ giác đã được học trên lớp

Xem chi tiết!

Đề bài 2 trang 66 SGK Toán 8 tập 1

Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác.

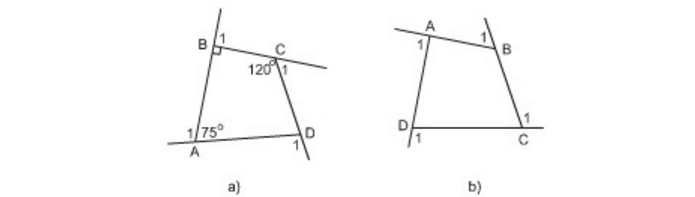
a) Tính các góc ngoài của tứ giác ở hình 7a.

b) Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài): \(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = ?\)

c) Có nhận xét gì về tổng các góc ngoài của tứ giác?

» Bài tập trước: Bài 1 trang 66 sgk Toán 8 tập 1

Giải bài 2 trang 66 sgk Toán 8 tập 1

Hướng dẫn cách làm

+) Áp dụng định lý: Tổng các góc trong tứ giác bằng \({360^0}\)

+) Áp dụng tính chất: Tổng hai góc kề bù bằng \({180^0}\)

Bài giải chi tiết

Dưới đây là các cách giải bài 2 trang 66 SGK Toán 8 tập 1 để các bạn tham khảo và so sánh bài làm của mình:

a) \(\widehat A + \widehat B + \widehat C + \widehat D = {360^0}\) (định lý tổng các góc của tứ giác)

\(\begin{array}{l} \widehat {{D}}= {360^0} - \left( {\widehat A + \widehat B + \widehat C} \right)\\ = {360^0} - \left( {{75}^0+{{90}^0} + {{120}^0}} \right)\\ = {360^0} - {285^0}\\= {75^0} \end{array}\)

Ta có:

+) \( \widehat {BAD} + \widehat {{A_1}} = {180^0}\) (2 góc kề bù)

\(\begin{array}{l} \widehat {{A_1}} = {180^0} - \widehat {BAD}\\ = {180^0} - {75^0} = {105^0}. \end{array}\)

+) \(\widehat {{B_1}} + \widehat {CBA} = {180^0} \)(2 góc kề bù)

\(\begin{array}{l} \widehat {{B_1}} = {180^0} - \widehat {CBA}\\= {180^0} - {90^0} = {90^0}. \end{array}\)

+) \(\widehat {{C_1}} + \widehat {BCD} = {180^0}\) (2 góc kề bù)

\(\begin{array}{l} \widehat {{C_1}} = {180^0} - \widehat {BC{\rm{D}}}\\= {180^0} - {120^0} = {60^0}. \end{array}\)

+) \( \widehat {{D_1}} + \widehat {ADC} = {180^0}\)

\(\begin{array}{l} \widehat {{D_1}} = {180^0} - \widehat {{\rm{ADC}}}\\= {180^0} - {75^0} = {105^0}. \end{array}\)

b) \(\widehat {{A}} + \widehat {{B}} + \widehat {{C}} + \widehat {{D}} = {360^0}\)

(định lý tổng 4 góc trong tứ giác)

\(\begin{array}{l} \widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}}\\ = \left( {{{180}^0} - \widehat {{A}}} \right) + \left( {{{180}^0} - \widehat {{B}}} \right) \\\;\;\;+ \left( {{{180}^0} - \widehat {{C}}} \right) + \left( {{{180}^0} - \widehat {{D}}} \right)\\ = {180^0}.4 - \left( {\widehat {{A}} + \widehat {{B}} + \widehat {{C}} + \widehat {{D}}} \right)\\ = {720^0} - {360^0} = {360^0}. \end{array}\)

c) Nhận xét: Tổng các góc ngoài của tứ giác bằng \({360^0} \)

» Bài tập tiếp theo: Bài 3 trang 67 sgk Toán 8 tập 1

Ghi nhớ

Tổng bốn góc trong một tứ giác bằng 360º

Hai góc kề bù có tổng bằng 180º.

Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 2 trang 66 sgk toán 8 tập 1. Mong rằng những bài hướng dẫn giải toán 8 của Đọc Tài Liệu sẽ là người đồng hành giúp các bạn học tốt môn học này.