Bài 61 trang 91 SGK Toán 9 tập 2

Bạn muốn giải bài 61 trang 91 SGK Toán 9 tập 2 không nên bỏ qua bài viết này. Với những hướng dẫn chi tiết, không chỉ tham khảo cách làm hoặc đáp án mà bài viết này còn giúp bạn nắm vững lại các kiến thức Toán 9 chương 3 phần hình học để tự tin giải tốt các bài tập khác về đường tròn ngoại tiếp, đường tròn nội tiếp.

Đề bài 61 trang 91 SGK Toán 9 tập 2

a) Vẽ đường tròn tâm $O$, bán kính $2cm$.

b) Vẽ hình vuông nội tiếp đường tròn $(O)$ ở câu a)

c) Tính bán kính $r$ của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn $(O;r)$.

» Bài tập trước: Bài 60 trang 90 SGK Toán 9 tập 2

Giải bài 61 trang 91 SGK Toán 9 tập 2

Hướng dẫn cách làm

+) Sử dụng compa và thước kẻ để vẽ hình.

+) Sử dụng định lý Pi-ta-go để tính $r.$

Đáp án chi tiết

Dưới đây là các cách giải bài 61 trang 91 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

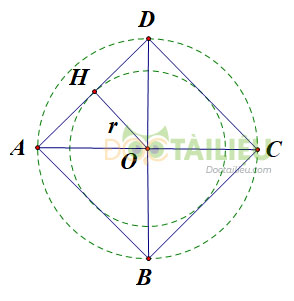
a) Chọn điểm $O$ làm tâm, mở compa có độ dài $2cm$ vẽ đường tròn tâm $O$, bán kính $2cm$: $(O; 2cm).$

Vẽ bằng eke và thước thẳng.

b) Vẽ đường kính $AC$ và $BD$ vuông góc với nhau. Nối $A$ với $B$, $B$ với $C$, $C$ với $D$, $D$ với $A$ ta được tứ giác $ABCD$ là hình vuông nội tiếp đường tròn $(O;2cm)$

c) Kẻ $OH \bot AD.$

Khi đó ta có $OH$ là bán kính $r$ của đường tròn nội tiếp hình vuông $ABCD$.

Ta có: $\Delta OAD$ là tam giác vuông cân tại $O$ lại có $OH$ là đường cao $\Rightarrow \, H$ là trung điểm của $AD \Rightarrow OH=AH=HD.$

$\Rightarrow r = OH = AH.$

Áp dụng định lý Pi-ta-go cho tam giác vuông $OHD$ ta có:

$OH^2+AH^2=OA^2$ $\Leftrightarrow {r^2} + {r^2}  = {2^2} \Rightarrow 2{r^2} = 4 \Rightarrow r = \sqrt 2 (cm).$

Vẽ đường tròn $(O;\sqrt2cm)$. Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh.

» Bài tiếp theo: Bài 62 trang 91 SGK Toán 9 tập 2

Trên đây là hướng dẫn cách làm và đáp án bài 61 trang 91 Toán hình học 9 tập 2. Các em cũng có thể tham khảo thêm các bài tập tại chuyên mục giải Toán 9 của doctailieu.com.