Hệ thống kiến thức lý thuyết tiết đường tròn ngoại tiếp, đường tròn nội tiếp và các dạng toán thường gặp cùng hướng dẫn chi tiết cách làm giúp các em nắm được kiến thức từ khái quát đến chi tiết để học tốt phần kiến thức này.
Mời các em cùng tham khảo:

I. Lý thuyết đường tròn ngoại tiếp, đường tròn nội tiếp
Định nghĩa
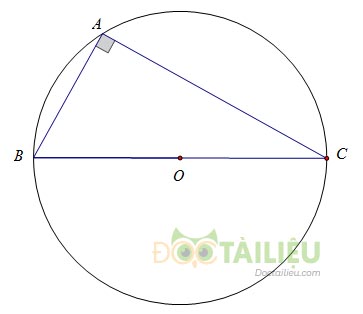
Ví dụ: Đường tròn \(\left( O \right)\) ngoại tiếp tam giác ABC và tam giác ABC nội tiếp đường tròn \(\left( O \right)\) .
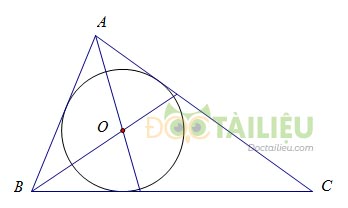
Ví dụ: Đường tròn \(\left( O \right)\) nội tiếp tam giác ABC và tam giác ABC ngoại tiếp đường tròn \(\left( O \right)\)
Định lý
II. Các dạng toán thường gặp về đường tròn ngoại tiếp, đường tròn nội tiếp
Dạng 1: Xác định tâm, bán kính và các đại lượng liên quan của đường tròn ngoại tiếp, đường tròn nội tiếp
Phương pháp:
Sử dụng các kiến thức về đường tròn nội tiếp và đường tròn ngoại tiếp đồng thời vận dụng linh hoạt các hệ thức lượng để tính toán.
III. Bài tập về đường tròn ngoại tiếp, đường tròn nội tiếp
Trong đường tròn (O; R) cho một dây AB bằng cạnh hình vuông nội tiếp và dây BC bằng cạnh tam giác đều nội tiếp (điểm C và điểm A ở cùng một phía đối với BO). Tính các cạnh của tam giác ABC và đường cao AH của nó theo R.
Lời giải:
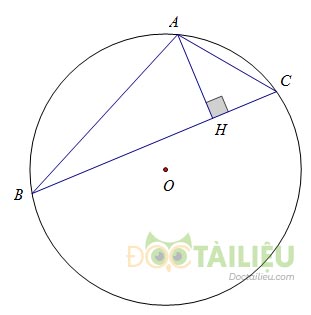
Dây AB bằng cạnh hình vuông nội tiếp đường tròn (O; R) nên \(AB = R\sqrt 2 \)
và cung \(\overparen{AB}\) nhỏ có \(sđ \overparen{AB}=90^\circ\).
Dây BC bằng cạnh hình tam giác đều nội tiếp đường tròn (O; R) nên \(BC = R\sqrt 3\) và cung nhỏ \(\overparen{BC}\) có \(sđ \overparen{BC}= 120^\circ .\)
\( \Rightarrow sđ \overparen{AC} = sđ \overparen{BC} - sđ \overparen{AB} =120^\circ - 90^\circ = 30^\circ \)
\( \Rightarrow \widehat {ABC} = \displaystyle {1 \over 2} sđ \overparen{AC}=15^\circ\) (tính chất góc nội tiếp)
Trong \(∆AHB\) có \(\widehat {AHB} = 90^\circ \)
\( \Rightarrow AH = AB.\sin \widehat {ABH} = R\sqrt 2 .\sin 15^\circ \approx 0,36R\)
Trong \(∆AHC\) có \(\widehat {AHC} = 90^\circ\)
\(\widehat {ACB} = \displaystyle{1 \over 2} sđ \overparen{AB}=45^\circ\) (tính chất góc nội tiếp)
\(AC =\displaystyle {{AH} \over {\sin \widehat {ACH}}} =\displaystyle {{AH} \over {\sin 45^\circ }} \approx {{0,36R} \over {\sin 45^\circ }} \approx 0,51R \)
=>> Xem thêm nhiều bài tập khác trong Toán hình 9 chương 3 bài 8 để củng cố kiến thức và rèn luyện kỹ năng làm bài
*************
Trên đây là lý thuyết đường tròn ngoại tiếp, đường tròn nội tiếp bao gồm các kiến thức cần nắm và những dạng bài liên quan. Hy vọng đây sẽ là tài liệu hữu ích phục vụ việc học tập của các em. Ngoài ra, các em hãy truy cập doctailieu.com để tham khảo thêm nhiều tài liệu học Toán lớp 9 phong phú khác mà chúng tôi đã sưu tầm và tổng hợp nhé. Chúc các em luôn học tốt và đạt kết quả cao!