Bài 62 trang 91 SGK Toán 9 tập 2

Đáp án bài 62 trang 91 SGK Toán 9 tập 2 được biên soạn bởi Đọc Tài Liệu nhằm mục đích tham khảo phương pháp làm bài. Tài liệu cũng giúp các bạn ôn tập nội dung kiến thức trong Toán 9 chương 3 phần hình học về đường tròn ngoại tiếp, đường tròn nội tiếp.

Đề bài 62 trang 91 SGK Toán 9 tập 2

a) Vẽ tam giác \(ABC\) cạnh \(a = 3cm\).

b) Vẽ đường tròn \((O;R)\) ngoại tiếp tam giác đều \(ABC\). Tính \(R\).

c) Vẽ đường tròn \((O;r)\) nội tiếp tam giác đều \(ABC\). Tính \(r\).

d) Vẽ tiếp tam giác đều \(IJK\) ngoại tiếp đường tròn \((O;R)\).

» Bài tập trước: Bài 61 trang 91 SGK Toán 9 tập 2

Giải bài 62 trang 91 SGK Toán 9 tập 2

Hướng dẫn cách làm

+) Sử dụng thước và compa để vẽ hình.

+) Tâm đường tròn ngoại tiếp là giao của 3 đường trung trực.

+) Tâm đường tròn nội tiếp là giao của 3 đường phân giác.

+) Sử dụng định lý Pi-ta-go và tính chất của tam giác đều để tính R và r.

Đáp án chi tiết

Dưới đây là các cách giải bài 62 trang 91 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

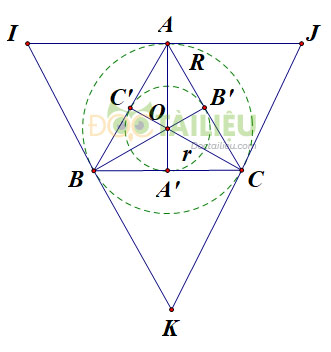
a) Vẽ tam giác đều \(ABC\) có cạnh bằng \(3cm\) (dùng thước có chia khoảng và compa).

b) Gọi \(A';B';C'\) lần lượt là trung điểm của \(BC;AC;AB.\)

Tâm \(O\) của đường tròn ngoại tiếp tam giác đều \(ABC\) là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác \(AA';BB';CC'\) của tam giác đều \(ABC\)).

Tính \(AA'\):

Xét tam giác \(AA'C\) vuông tại \(A'\) có \(AC=3;A'C=\dfrac{3}{2}\), theo định lý Pytago ta có \(AC^2=AA'^2+A'C^2\)\(\Rightarrow AA'^2=3^2-\dfrac {3^2}{4}=\dfrac {9}{4} \Rightarrow AA'=\dfrac {3\sqrt {3}}{2}\)

Ta có bán kính đường tròn ngoại tiếp tam giác ABC là   \(R= OA =\) \(\dfrac{2}{3}\)\(AA'\) = \(\dfrac{2}{3}\). \(\dfrac{3\sqrt{3}}{2}\) = \(\sqrt3 (cm)\).

c) Đường tròn nội tiếp \((O;r)\) tiếp xúc ba cạnh của tam giác đều \(ABC\) tại các trung điểm \(A', B', C'\) của các cạnh.

Ta có: \(r = OA' = \)\(\dfrac{1}{3}\)\( AA'\) =\(\dfrac{1}{3}\) \(\dfrac{3\sqrt{3}}{2}\) = \(\dfrac{\sqrt{3}}{2}(cm).\)

d) Vẽ các tiếp tuyến với đường tròn \((O;R)\) tại \(A,B,C\). Ba tiếp tuyến này cắt nhau tại \(I, J, K\). Ta có \(∆IJK\) là tam giác đều ngoại tiếp \((O;R)\).

» Bài tiếp theo: Bài 63 trang 92 SGK Toán 9 tập 2

Trên đây là nội dung hướng dẫn trả lời bài 62 trang 91 SGK Toán 9 tập 2 được Đọc Tài Liệu chia sẻ để giúp bạn hoàn thành tốt bài làm của mình. Mong rằng những tài liệu giải Toán 9 của chúng tôi sẽ luôn là người bạn đồng hành để giúp bạn học tốt hơn môn học này.