Bài 60 trang 92 SGK Toán 8 tập 2

Bạn tìm tài liệu hướng dẫn giải bài 60 trang 92 SGK Toán 8 tập 2? không cần tìm nữa...

Những nội dung dưới đây không chỉ giúp bạn biết được cách làm, tham khảo đáp án... mà còn hỗ trợ bạn ôn tập để nắm vững các kiến thức toán 8 chương 3 phần hình học Tam giác đồng dạng đã được học trên lớp

Xem chi tiết!

Đề bài 60 trang 92 SGK Toán 8 tập 2

Cho tam giác vuông \(ABC\), và đường phân giác \(BD\) (\(D\) thuộc cạnh \(AC\)).

a) Tính tỉ số \(\dfrac{{A{\rm{D}}}}{{C{\rm{D}}}}\) .

b) Cho biết độ dài \(AB = 12,5 cm\). Hãy tính chu vi và diện tích của tam giác \(ABC\).

» Bài tập trước: Bài 59 trang 92 SGK Toán 8 tập 2

Giải bài 60 trang 92 sgk Toán 8 tập 2

Hướng dẫn cách làm

Áp dụng: Tính chất đường phân giác của tam giác, định lí Pitago, công thức tính chu vi và diện tích của tam giác.

Bài giải chi tiết

Dưới đây là các cách giải bài 60 trang 92 SGK Toán 8 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

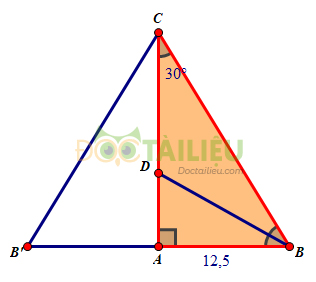
a) Xét tam giác \(BCA\) vuông tại \(A\) (gt) có:

\(\begin{array}{l} \widehat {ACB} + \widehat {ABC} = {90^0}\\ \Rightarrow \widehat {ABC} = {90^0} - \widehat {ACB} \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;= {90^0} - {30^0} = {60^0} \end{array}\)

Trên tia đối của tia \(AB\) lấy điểm \(B'\) sao cho \(AB = AB'\) (1)

Xét hai tam giác vuông \(ABC\) và \(AB'C\) có:

\(AC\) chung (gt)

\(AB = AB'\) (gt)

\( \Rightarrow \Delta ABC = \Delta AB'C\) (cạnh góc vuông - cạnh góc vuông)

\( \Rightarrow BC = B'C\) (2 cạnh tương ứng)

\( \Rightarrow \Delta BB'C\) cân tại \(C\).

Lại có \(\widehat {ABC} = {60^0}\) nên suy ra \(\Delta BB'C\) đều (dấu hiệu nhận biết tam giác đều) (2)

Từ (1) và (2) \( \Rightarrow \dfrac{{AB}}{{BC}} = \dfrac{1}{2}\)

Vì \(BD\) là đường phân giác của \(\Delta ABC\) nên:

\(\dfrac{{DA}}{{DC}} = \dfrac{{BA}}{{BC}} = \dfrac{1}{2}\)

b) \(∆ABC\) vuông tại \(A\) nên áp dụng định lí Pitago ta có:

\(\eqalign{ & A{C^2} = B{C^2} - A{B^2},\,BC = 2AB \cr & \Rightarrow A{C^2} = 4A{B^2} - A{B^2} = 3A{B^2} \cr & \Rightarrow AC = \sqrt {3A{B^2}} = AB\sqrt 3 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 12,5\sqrt 3 \approx 21,65\,cm \cr} \)

Gọi \(p\) là chu vi \(∆ABC\)

\( \Rightarrow p = AB + BC + CA\)

\( \Rightarrow p = 3AB + AC = 3.12,5 + 12,5\sqrt 3 \)

\( \Rightarrow p = 12,5 (3+\sqrt 3 ) \approx 59,15\left( {cm} \right)\)

\({S_{ABC}} = \dfrac{1 }{ 2}AB.AC \approx 135,31(c{m^2})\)

» Bài tập tiếp theo: Bài 61 trang 92 SGK Toán 8 tập 2

Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 60 trang 92 sgk toán 8 tập 2. Mong rằng những bài hướng dẫn giải toán 8 của Đọc Tài Liệu sẽ là người đồng hành giúp các bạn học tốt môn học này.