Tổng hợp lý thuyết chương 3 phần Hình học: Tam giác đồng dạng

Bạn đang tìm kiếm tài liệu tổng hợp kiến thức về tam giác đồng dạng? Hãy tham khảo ngay bài viết dưới đây của Đọc tài liệu với những lý thuyết chương 3 phần Hình học: Tam giác đồng dạng. Đây sẽ là tài liệu học tập hữu ích cho học sinh và đồng thời giúp các thầy cô có thêm tài liệu hay phục vụ việc dạy học.

Cùng tham khảo nhé!

Tổng hợp kiến thức cần nắm chương 3 phần Hình học: Tam giác đồng dạng

1.Tỉ số của hai đoạn thẳng

- Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.

- Tỉ số của hai đoạn thẳng không phụ thuộc vào cách chọn đơn vị đo.

2. Đoạn thẳng tỉ lệ

Hai đoạn thẳng \(AB\)  và \(CD\) tỉ lệ với hai đoạn thẳng \(A'B'\)và\( C'D'\) nếu có tỉ lệ thức:

\(\dfrac{{AB}}{{C{\rm{D}}}} = \dfrac{{A'B'}}{{C'D'}}\)   hay     \(\dfrac{{AB}}{{A'B'}} = \dfrac{{C{\rm{D}}}}{{C'D'}}\)

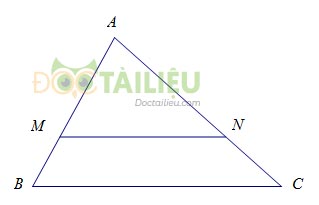
3. Định lí Ta-lét trong tam giác

a) Định lí Ta-lét trong tam giác

b) Định lí Ta-lét đảo

c) Hệ quả định lý Ta-lét

Chú ý: Hệ quả trên vẫn đúng cho trường hợp đường thẳng song song với một cạnh và cắt phần kéo dài của hai cạnh còn lại.

4. Tính chất đường phân giác trong tam giác

Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.

\(AD,{\rm{ }}AE\) là các phân giác trong và ngoài của góc, suy ra: \( \dfrac{{DB}}{{DC}} = \dfrac{{AB}}{{AC}} = \dfrac{{EB}}{{EC}}\)

5. Nhắc lại một số tính chất của tỉ lệ thức

\(\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow \left\{ \begin{array}{l}a{\rm{d}} = bc\\\dfrac{a}{c} = \dfrac{b}{d}\\\dfrac{{a \pm b}}{b} = \dfrac{{c \pm d}}{d}\\\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{a + c}}{{b + d}} = \dfrac{{a - c}}{{b - d}}\end{array} \right.\)

6. Khái niệm hai tam giác đồng dạng

a. Định nghĩa:

Hai tam giác gọi là đồng dạng với nhau nếu chúng có ba cặp góc bằng nhau từng đôi một và ba cặp cạnh tương ứng tỉ lệ.

\( \Delta ABC \backsim \Delta A'B'C'\) \(\Leftrightarrow \left\{ \begin{array}{l}\widehat A = \widehat {A'},\,\widehat B = \widehat {B'},\widehat C = \widehat {C'}\\\dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{CA}}{{C'A'}}\end{array} \right.\)

* Tỉ số các cạnh tương ứng \(\dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{CA}}{{C'A'}} = k\) được gọi là tỉ số đồng dạng  của hai tam giác.

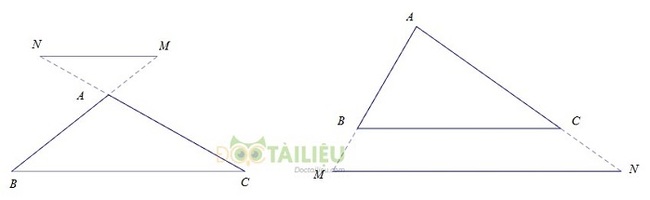
b. Định lí: Nếu một đường thẳng cắt hai cạnh của tam giác và song song với hai cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.

Chú ý: Định lí trên cũng đúng trong trường hợp đường thẳng a cắt phần kéo dài hai cạnh của tam giác và song song với cạnh còn lại.

6. Các trường hợp đồng dạng của hai tam giác

7. Các trường hợp đồng dạng của tam giác vuông

8. Tính chất của hai tam giác đồng dạng

Nếu hai tam giác đồng dạng với nhau thì:

+ Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng.

+ Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng.

+ Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng.

+ Tỉ số các chu vi bằng tỉ số đồng dạng.

- Tỉ số các diện tích bằng bình phương tỉ số đồng dạng.

*********************

Hy vọng với hệ thống kiến thức lý thuyết chương 3 phần Hình học: Tam giác đồng dạng trên đây, các em sẽ có thêm một tài liệu học tập hữu ích để học tốt hơn môn Toán 8. Chúc các em luôn học tốt và đạt kết quả cao!