Bài 33 trang 77 SGK Toán 8 tập 2

Bạn tìm tài liệu hướng dẫn giải bài 33 trang 77 SGK Toán 8 tập 2? không cần tìm nữa...

Những nội dung dưới đây không chỉ giúp bạn biết được cách làm, tham khảo đáp án... mà còn hỗ trợ bạn ôn tập để nắm vững các kiến thức Toán 8 chương 3 phần hình học về trường hợp đồng dạng thứ hai đã được học trên lớp

Xem chi tiết!

Đề bài 33 trang 77 SGK Toán 8 tập 2

Chứng minh rằng nếu tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\) theo tỉ số \(k\), thì tỉ số của hai đường trung tuyến tương ứng với hai tam giác đó cũng bằng \(k\).

» Bài tập trước: Bài 32 trang 77 sgk Toán 8 tập 2

Giải bài 33 trang 77 sgk Toán 8 tập 2

Hướng dẫn cách làm

Áp dụng:

- Định lí: Nếu hai cạnh tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp đó bằng nhau, thì hai tam giác đồng dạng.

- Tính chất hai tam giác đồng dạng.

- Tính chất trung tuyến.

Bài giải chi tiết

Dưới đây là các cách giải bài 33 trang 77 SGK Toán 8 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

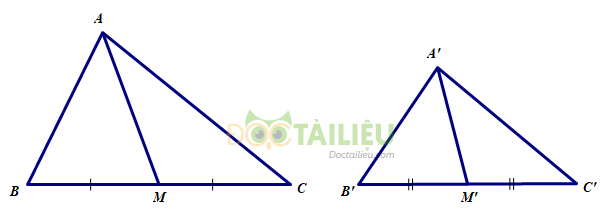
Giả sử \(∆A'B'C'\) đồng dạng \(∆ABC\) theo tỉ số \(k, AM, A'M'\) là hai đường trung tuyến tương ứng.

Vì \(∆A'B'C'\) đồng dạng \(∆ABC\) (giả thiết)

\(\dfrac{A'B'}{AB} = \dfrac{B'C'}{BC}\) (tính chất hai tam giác đồng dạng)

Mà \(B'C' = 2B'M', BC = 2BM\) (tính chất trung tuyến)

\( \Rightarrow \dfrac{{A'B'}}{{AB}} = \dfrac{{2B'M'}}{{2BM}} = \dfrac{{B'M'}}{{BM}}\)

Xét  \(∆ABM\) và \( ∆A'B'M'\) có:

\(\widehat{B} = \widehat{B'}\) (vì \(∆A'B'C'\) đồng dạng \(∆ABC\))

\( \dfrac{{A'B'}}{{AB}} = \dfrac{{B'M'}}{{BM}}\) (chứng minh trên)

\( \Rightarrow ∆A'B'M' \) đồng dạng \(∆ABM\) (c-g-c)

\( \Rightarrow \dfrac{A'M'}{AM}= \dfrac{A'B'}{AB} = k.\)

» Bài tập tiếp theo: Bài 34 trang 77 sgk Toán 8 tập 2

Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 33 trang 77 sgk toán 8 tập 2. Mong rằng những bài hướng dẫn giải toán 8 của Đọc Tài Liệu sẽ là người đồng hành giúp các bạn học tốt môn học này.