Bài 25 trang 55 SGK Toán 9 tập 1

Bạn muốn giải bài 25 trang 55 SGK Toán 9 tập 1 không nên bỏ qua bài viết này. Với những hướng dẫn chi tiết, không chỉ tham khảo cách làm hoặc đáp án mà bài viết này còn giúp bạn nắm vững lại các kiến thức Toán 9 bài 4 để tự tin giải tốt các bài tập về Đường thẳng song song và đường thẳng cắt nhau

Đề bài 25 trang 55 SGK Toán 9 tập 1

a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ:

\(y = \dfrac{2}{3}x + 2\);                                       \(y =  - \dfrac{3}{2}x + 2\)

b) Một đường thẳng song song với trục hoành \(Ox\), cắt trục tung \(Oy\) tại điểm có tung độ bằng \(1\), cắt các đường thẳng \(y = \dfrac{2}{3}x + 2\) và \(y =  - \dfrac{3}{2}x + 2\) theo thứ tự tại hai điểm \(M\) và \(N\). Tìm tọa độ của hai điểm \(M\) và \(N\).

» Bài tập trước: Bài 24 trang 55 SGK Toán 9 tập 1

Giải bài 25 trang 55 SGK Toán 9 tập 1

Hướng dẫn cách làm

a) Cách vẽ đồ thị hàm số \(y=ax+b,\ (a \ne 0)\): Đồ thị hàm số \(y=ax+b \, \, (a\neq 0)\) là đường thẳng:

+) Cắt trục hoành tại điểm \(A(-\dfrac{b}{a}; \, 0).\)

+) Cắt trục tung tại điểm \(B(0;b).\)

Xác định tọa độ hai điểm \(A\) và \(B\) sau đó kẻ đường thẳng đi qua hai điểm đó ta được đồ thị hàm số  \(y=ax+b \, \, (a\neq 0).\)

b) +) Đường thẳng song song với trục \(Ox\) có dạng \(y=a\), đường thẳng song song với trục \(Oy\) có dạng \(x=b\).

+) Hai đường thẳng \(y=ax+b,\ y=a'x+b'\) cắt nhau tại \(A\). Hoành độ điểm \(A\) là nghiệm của phương trình: \(ax+b=a'x+b\). Giải phương trình tìm \(x\). Thay \(x\) tìm được vào công thức hàm số trên tìm được tung độ điểm \(A\).

Đáp án chi tiết

Dưới đây là các cách giải bài 25 trang 55 SGK Toán 9 tập 1 để các bạn tham khảo và so sánh bài làm của mình:

a) Hàm số \(y = \dfrac{2}{3}x + 2\)

Cho \(x= 0 \Rightarrow y = \dfrac{2}{3}. 0+ 2=0+2=2 \Rightarrow A(0; 2)\)

Cho \(y= 0 \Rightarrow 0 = \dfrac{2}{3}. x+ 2 \Rightarrow x=-3 \Rightarrow B(-3; 0)\)

Đường thẳng đi qua hai điểm \(A,\ B\) là đồ thị của hàm số \(y = \dfrac{2}{3}x + 2\).

+) Hàm số \(y =- \dfrac{3}{2}x + 2\)

Cho \(x= 0 \Rightarrow y = -\dfrac{3}{2}. 0+ 2=0+2=2 \Rightarrow A(0; 2)\)

Cho \(y=0 \Rightarrow y = -\dfrac{3}{2}. 0+ 2 \Rightarrow x= \dfrac{4}{3}  \Rightarrow C {\left(\dfrac{4}{3}; 0 \right)}\)

Đường thẳng đi qua hai điểm \(A,\ C\) là đồ thị của hàm số \(y = -\dfrac{3}{2}x + 2\).

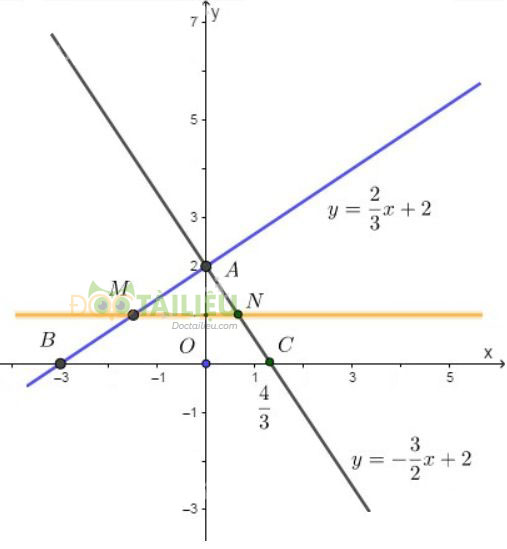
» Bài tiếp theo: Bài 26 trang 55 SGK Toán 9 tập 1

b) Đường thẳng song song với trục \(Ox\) cắt trục \(Oy\) tại điểm có tung độ \(1\) có dạng: \(y=1\).

Vì \(M\) là giao của đường thẳng \(y=\dfrac{2}{3}x+2\) và \(y=1\) nên hoành độ của \(M\) là nghiệm của phương trình:

\(\dfrac{2}{3}x+2=1\)

\(\Leftrightarrow \dfrac{2}{3}x=1-2\)

\(\Leftrightarrow \dfrac{2}{3}x=-1\)

\(\Leftrightarrow x=-\dfrac{3}{2}\)

Do đó tọa độ \(M\) là: \(M{\left( -\dfrac{3}{2}; 1 \right)}\).

Vì \(N\) là giao của đường thẳng \(y=-\dfrac{3}{2}x+2\) và \(y=1\) nên hoành độ của \(N\) là nghiệm của phương trình:

\(-\dfrac{3}{2}x+2=1\)

\(\Leftrightarrow -\dfrac{3}{2}x=1-2\)

\(\Leftrightarrow -\dfrac{3}{2}x=-1\)

\(\Leftrightarrow x=\dfrac{2}{3}\)

Do đó tọa độ \(N\) là: \(N{\left( \dfrac{2}{3}; 1 \right)}\).

Giải bài tập khác

Xem thêm hướng dẫn giải các bài tập khác

• Bài 29 trang 59 SGK Toán 9 tập 1
• Bài 20 trang 54 SGK Toán 9 tập 1

Trên đây là nội dung hướng dẫn trả lời bài 25 trang 55 SGK Toán 9 tập 1 được Đọc Tài Liệu chia sẻ để giúp bạn hoàn thành tốt bài làm của mình. Mong rằng những tài liệu giải Toán 9 của chúng tôi sẽ luôn là người bạn đồng hành để giúp bạn học tốt hơn môn học này.