Bài 10 trang 63 SGK Toán 8 tập 2

Tài liệu hướng dẫn giải bài 10 trang 63 sgk Toán 8 tập 2 này giúp bạn biết được cách làm để hoàn thành tốt bài tập và nắm vững các kiến thức quan trọng của chương 3 phần hình học định lí đảo và hệ quả của định lí Ta - let đã được học trên lớp.

Đề bài 10 trang 63 SGK Toán 8 tập 2

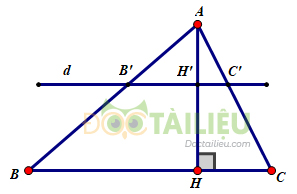
$∆ABC$ có đường cao $AH$. Đường thẳng $d$ song song với $BC$, cắt các cạnh $AB, AC$ và đường cao $AH$ theo thứ tự tại các điểm $B', C'$ và $H'$(h.16)

a) Chứng minh rằng:

$\dfrac{AH'}{AH}= \dfrac{B'C'}{BC}$.

b) Áp dụng: Cho biết $AH' = \dfrac{1}{3} AH$ và diện tích $∆ABC$ là $67,5$ cm²

Tính diện tích $∆AB'C'$.

» Bài tập trước: Bài 9 trang 63 sgk Toán 8 tập 2

Giải bài 10 trang 63 sgk Toán 8 tập 2

Hướng dẫn cách làm

Áp dụng: Hệ quả của định lý TaLet và công thức tính diện tích tam giác.

Bài giải chi tiết

Dưới đây là các cách giải bài 10 trang 63 SGK Toán 8 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

a) Chứng minh $\dfrac{AH'}{AH} = \dfrac{B'C'}{BC}$

Vì $B'C' // BC$ $\Rightarrow \dfrac{B'C'}{BC} = \dfrac{AB'}{AB}$   (1) (theo hệ quả định lý TaLet)

Trong $∆ABH$ có $BH' // BH$ $\Rightarrow \dfrac{AH'}{AH} = \dfrac{AB'}{AB}$  (2) (định lý TaLet)

Từ (1) và (2) $\Rightarrow \dfrac{B'C'}{BC} = \dfrac{AH'}{AH}$

b) $B'C' // BC$ mà $AH ⊥ BC$ nên $AH' ⊥ B'C'$ hay $AH'$ là đường cao của $∆AB'C'$.

Giả thiết: $AH' = \dfrac{1}{3} AH$.

Áp dụng kết quả câu a) ta có:

$\dfrac{B'C'}{BC}= \dfrac{AH'}{AH} = \dfrac{1}{3}$

$\Rightarrow  B'C' = \dfrac{1}{3} BC$

$\eqalign{ & {S_{AB'C'}} = {1 \over 2}AH'.B'C' \cr&\;\;\;\;\;\;\;\;\;\;\;= {1 \over 2}.{1 \over 3}AH.{1 \over 3}BC \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \;\;= {1 \over 9}.\left( {{1 \over 2}AH.BC} \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \;\;= {1 \over 9}.{S_{ABC}}\cr&\;\;\;\;\;\;\;\;\;\;\; = {1 \over 9}.67,5 = 7,5\,\,c{m^2} \cr}$

» Bài tập tiếp theo: Bài 11 trang 63 sgk Toán 8 tập 2

Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 10 trang 63 sgk toán 8 tập 2. Mong rằng những bài hướng dẫn giải toán 8 của Đọc Tài Liệu sẽ là người đồng hành giúp các bạn học tốt môn học này.