Bài 9 trang 63 SGK Toán 8 tập 2

Lời giải bài 9 trang 63 sgk Toán 8 tập 2 được chia sẻ với mục đích tham khảo cách làm và so sánh đáp án. Cùng với đó góp phần giúp bạn ôn tập lại các kiến thức Toán 8 chương 3 phần hình học để tự tin hoàn thành tốt các bài tập về định lí đảo và hệ quả của định lí Ta - let khác.

Đề bài 9 trang 63 SGK Toán 8 tập 2

Cho tam giác \(ABC\) và điểm \(D\) trên cạnh \(AB\) sao cho \(AD= 13,5cm, DB= 4,5cm\). Tính tỉ số các khoảng cách từ điểm \(D\) và \(B\) đến cạnh \(AC\).

» Bài tập trước: Bài 8 trang 63 sgk Toán 8 tập 2

Giải bài 9 trang 63 sgk Toán 8 tập 2

Hướng dẫn cách làm

Áp dụng: Hệ quả của định lý TaLet.

Bài giải chi tiết

Dưới đây là các cách giải bài 9 trang 63 SGK Toán 8 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

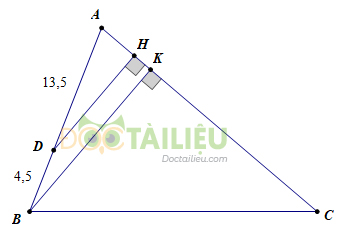
Gọi \(DH\) và \(BK\) lần lượt là khoảng cách từ \(B\) và \(D\) đến cạnh \(AC\).

Ta có \(DH // BK\) (vì cùng vuông góc với \(AC\))

\( \Rightarrow \dfrac{DH}{BK} = \dfrac{AD}{AB}\) (theo hệ quả định lý Ta Let)

Mà \(AB = AD + DB\) (giả thiết)

\( \Rightarrow  AB = 13,5 + 4,5 = 18\) (cm)

Vậy \(\dfrac{DH}{BK} = \dfrac{13,5}{18} = \dfrac{3}{4}\)

Vậy tỉ số khoảng cách từ điểm \(D\) và \(B\) đến \(AC\) bằng \(\dfrac{3}{4}\)

» Bài tập tiếp theo: Bài 10 trang 63 sgk Toán 8 tập 2

Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 9 trang 63 sgk toán 8 tập 2. Mong rằng những bài hướng dẫn giải toán 8 của Đọc Tài Liệu sẽ là người đồng hành giúp các bạn học tốt môn học này.