Đề thi tuyển sinh lớp 10 môn Toán tỉnh Thừa Thiên Huế năm học 2024 - 2025 chính thức được Đọc tài liệu cập nhật nhanh nhất kèm đáp án chi tiết. Tham khảo ngay nội dung đề thi và đáp án bên dưới.
Đề thi tuyển sinh 10 môn Toán Huế năm 2024
Đề thi và đáp án môn Toán kỳ thi vào lớp 10 năm 2024 tại tỉnh Thừa Thiên Huế sẽ được Đọc Tài Liệu cập nhật ngay khi môn thi kết thúc. Tham khảo đề thi và đáp án môn Toán tỉnh Thừa Thiên Huế các năm trước bên dưới:
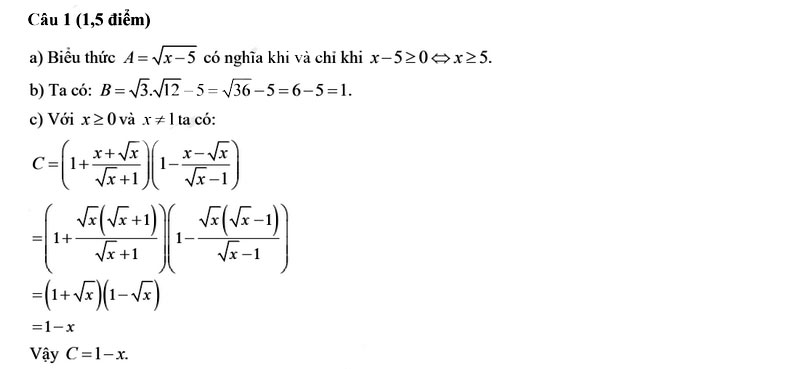





Đang cập nhật đáp án
Câu 3 (1,0 điểm) Hai học sinh cùng tham gia một giải chạy với hai cự li khác nhau, cự li của học sinh thứ nhất gấp đôi cự li của học sinh thứ hai (cự li là quãng đường mà người chạy phải hoàn thành). Biết rằng học sinh thứ nhất mất trung bình 5 phút để chạy hết 1 km, học sinh thứ hai mất trung bình 7 phút để chạy hết 1 km và thời gian hoàn thành cự li của học sinh thứ nhất nhiều hơn thời gian hoàn thành cự li của học sinh thứ hai là 15 phút. Tính cự li của mỗi học sinh tham gia.

Xem thêm thông tin
- Tra cứu điểm thi tuyển sinh lớp 10 năm 2024 Huế
- Điểm chuẩn lớp 10 năm 2024 Huế
- Đề thi tuyển sinh lớp 10 môn Văn Huế 2024
- Đề thi tuyển sinh lớp 10 môn Anh Huế 2024
Đề thi tuyển sinh lớp 10 môn Toán Huế năm 2023
ĐỀ THI

ĐÁP ÁN THAM KHẢO
Câu 1

Câu 2

Câu 3.

Câu 4

Câu 5
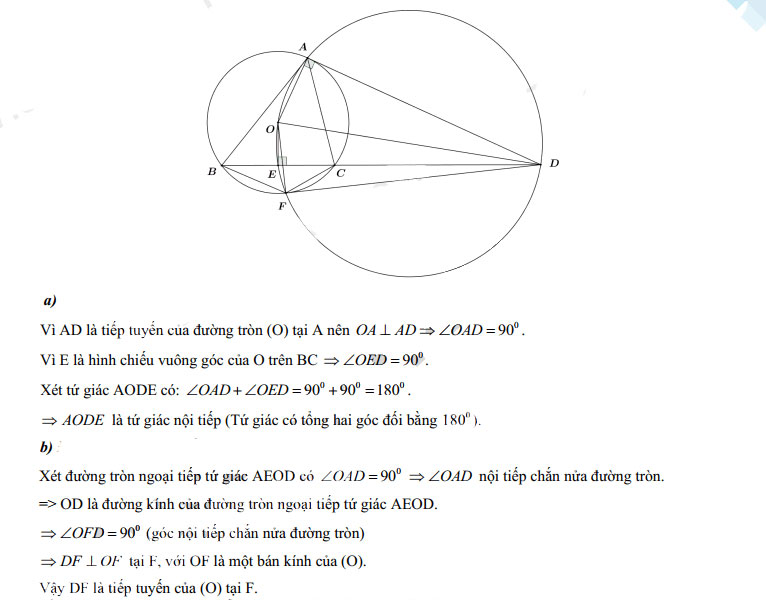

Câu 6.

Đề thi tuyển sinh lớp 10 môn Toán Thừa Thiên Huế năm 2022
ĐỀ THI

ĐÁP ÁN

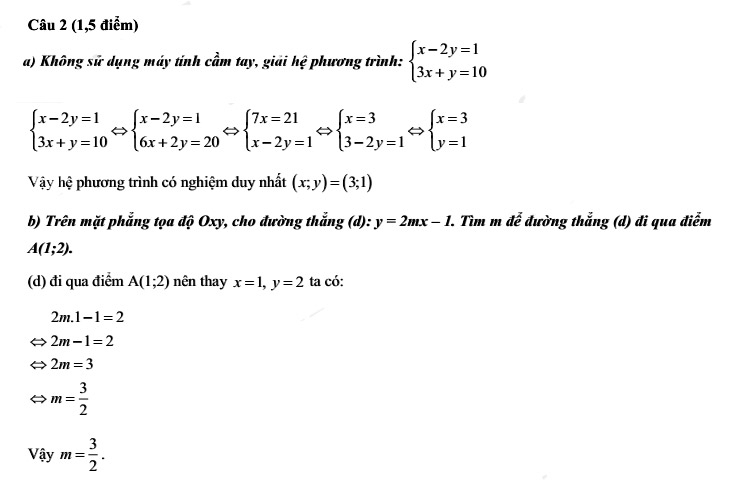
Câu 3.
Gọi x (giờ) là thời gian tổ A làm riêng sửa xong đoạn đường (x > 0)
=> Thời gian tổ B làm riêng để hoàn thành công việc là x + 12 (giờ)
Vì hai tổ cùng làm trong 8 giờ thì xong việc nên ta có phương trình
\(\begin{aligned} & \dfrac{1}{x}+\dfrac{1}{x+12}=\dfrac{1}{8} \\ \Leftrightarrow & 8(x+12)+8 x=x(x+12) \\ \Leftrightarrow & x^{2}-4 x-96=0 \\ \Leftrightarrow \quad & {\left[\begin{array}{l} x=12(\text { tmđk } \\ x=-8 \text { (ktmđk) } \end{array}\right.} \end{aligned}\)
Vậy nếu làm riêng thì tổ A làm trong 12 giờ, tổ B làm trong 12 + 12 = 24 giờ thì xong công việc.
Câu 4

Câu 5.
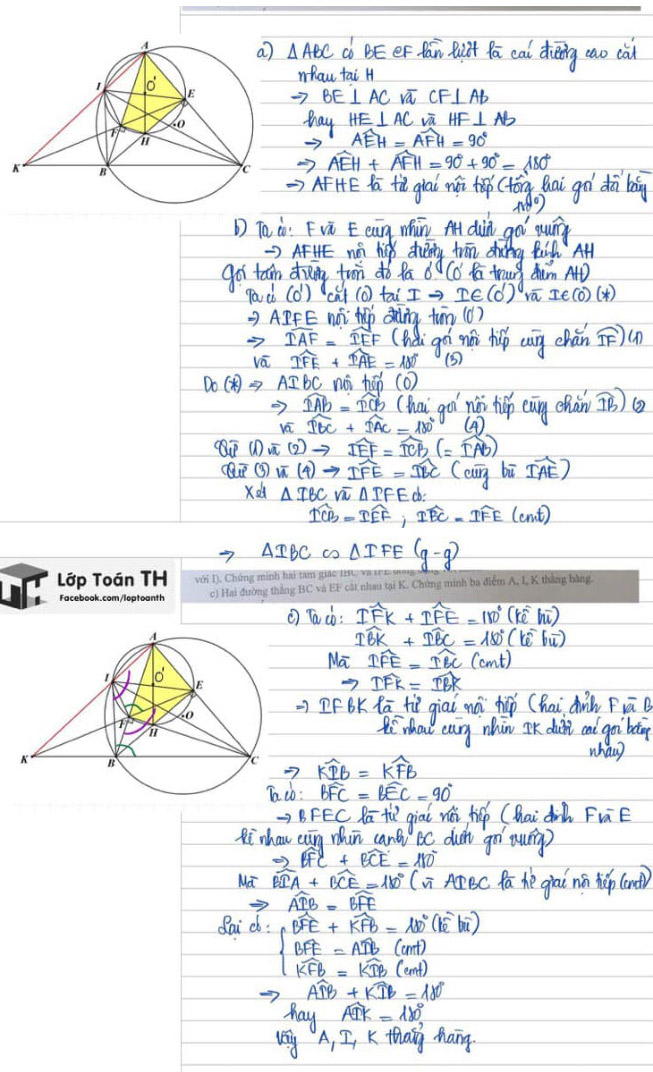
Câu 6

Đề thi Toán vào 10 Huế năm 2021

Đáp án đề thi vào lớp 10 môn Toán Huế 2021
Câu 1.
a) Với \( x \geq 0\) ta có \(\sqrt{x}=2 \Leftrightarrow(\sqrt{x})^{2}=2^{2} \Leftrightarrow x=4(t m)\) .
b)
\(\begin{aligned} &A=\sqrt{4.5}-\sqrt{9.5}+\sqrt{5} \\ &A=\sqrt{2^{2} \cdot 5}-\sqrt{3^{2} .5}+\sqrt{5} \\ &A=2 \sqrt{5}-3 \sqrt{5}+\sqrt{5} \\ &A=0 \\ \end{aligned}\)
Vậy A = 0
c)
\(\begin{aligned} &P=\frac{x \sqrt{x}+y \sqrt{y}}{\sqrt{x}+\sqrt{y}}-(\sqrt{x}-\sqrt{y})^{2} \\ &P=\frac{(\sqrt{x}+\sqrt{y})(x-\sqrt{x y}+y)}{\sqrt{x}+\sqrt{y}}-(x-2 \sqrt{x y}+y) \\ &P=x-\sqrt{x y}+y-x+2 \sqrt{x y}-y \\ &P=\sqrt{x y} \\ \end{aligned}\)
Vậy với x>0, y>0 thì \(P=\sqrt{x y} \).
Câu 2.
a. \(\left\{\begin{array} { l } { 3 x + y = 1 } \\ { x - 2 y = 5 } \end{array} \Leftrightarrow \left\{\begin{array} { l } { 6 x + 2 y = 2 } \\ { x - 2 y = 5 } \end{array} \Leftrightarrow \left\{\begin{array} { l } { 7 x = 7 } \\ { y = 1 - 3 x } \end{array} \Leftrightarrow \left\{\begin{array}{l} x=1 \\ y=1-3=-2 \end{array} .\right.\right.\right.\right.\)
Vây ...
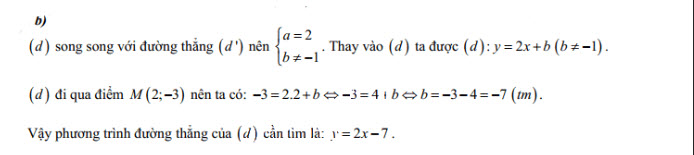
Câu 3

Câu 4

Câu 5.

Câu 6.
Thể tích ban đầu của khúc gỗ là: \(V_{1}=\pi \cdot 10^{2} \cdot 20=2000 \pi{cm}^{3}\)
Thể tich khối gỗ hình nón bị tiện bò là: \(V_{2}=\frac{1}{3} \pi \cdot 10^{2} \cdot 10=\frac{1000}{3} \pi{cm}^{3}\) .
Vậy thể tich phần khúc gỗ còn lại là \(V=V_{1}-V_{2}=2000 \pi-\frac{1000}{3} \pi=\frac{5000}{3} \pi \approx 5236{~cm}^{3} \).
-/-
Đề thi tuyển sinh lớp 10 môn Toán tỉnh Thừa Thiên Huế 2021-2022 chính thức được cập nhật ngay khi kỳ thi diễn ra ngày 05/06/2021.
Đáp án đề thi vào lớp 10 môn Toán Huế 2021
Đang cập nhật
Cùng ôn tập chuẩn bị thật tốt cho kỳ thi sắp tới với tuyển tập đề thi tuyển sinh lớp 10 môn Toán Huế nhé:
Tổng hợp đề thi tuyển sinh lớp 10 môn Toán Thừa Thiên Huế các năm trước
Đề thi tuyển sinh lớp 10 môn Toán năm 2020

Xem chi tiết đề thi và đáp án tại link: Đáp án đề thi tuyển sinh lớp 10 môn Toán Thừa Thiên Huế năm 2020
Đề thi vào 10 môn Toán năm 2019

Xem chi tiết đề thi và đáp án tại link: Đề thi vào lớp 10 môn Toán tỉnh Thừa Thiên Huế năm 2019 (có đáp án)
Đề Toán tuyển sinh lớp 10 năm 2018
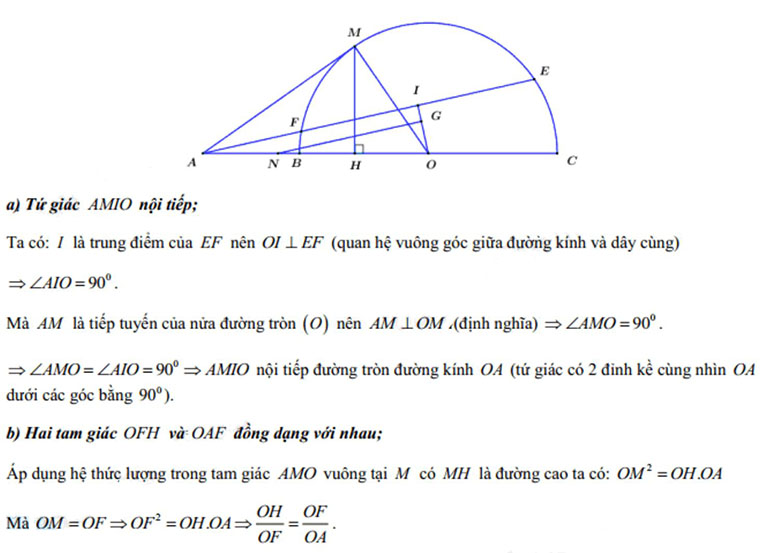
Câu 5: (3,0 điểm)
Cho tam giác ABC cân tại A. Gọi M là điểm bất kì nằm trên cạnh AC (M không trùng A và C). Một đường thẳng đi qua điểm M cắt cạnh BC tại I và cắt đường thẳng AB tại N sao cho I là trung điểm của đoạn thẳng MN. Đường phân giác trong của góc BAC cắt đường tròn ngoại tiếp tam giác AMN tại điểm D (D không trùng A). Chứng minh rằng:
a) DN = DM và DI vuông góc MN.
b) Tứ giác BNDI nội tiếp.
c) Đường tròn ngoại tiếp tam giác AMN luôn đi qua một điểm cố định (khác điểm A) khi M di chuyển trên cạnh AC.
Xem chi tiết đề thi và đáp án tại link: Đáp án đề thi lớp 10 môn Toán năm 2018 tỉnh Thừa Thiên Huế
Đọc tài liệu vừa gửi tới các em nội dung chi tiết để thi tuyển sinh vào 10 môn Toán Thừa Thiên Huế năm 2023 và tổng hợp đề thi vào 10 môn Toán các năm trước.
Mong rằng những tài liệu của chúng tôi sẽ là người đồng hành giúp các bạn hoàn thành tốt bài thi của mình.
Xem ngay: Tra cứu điểm thi tuyển sinh lớp 10
