Đọc tài liệu xin gửi tới các em đề thi vào 10 môn Toán năm 2024 từ Sở Giáo dục và Đào tạo tỉnh Đắk Lắk năm học 2023 - 2024 kèm đáp án chi tiết bên dưới. Các em hãy tham khảo đề cập nhật mới nhất bên dưới!
Đề thi tuyển sinh lớp 10 môn Toán Đắk Lắk 2024
Đề thi môn Toán kỳ thi vào lớp 10 năm 2024 tại tỉnh Đắk Lắk sẽ được Đọc Tài Liệu cập nhật ngay khi môn thi kết thúc.





Xem thêm thông tin:
- Tra cứu điểm thi tuyển sinh lớp 10 năm 2024 Đắk Lắk
- Điểm chuẩn lớp 10 năm 2024 Đắk Lắk
- Đáp án đề thi tuyển sinh lớp 10 môn Văn Đắk Lắk 2024
- Đáp án đề thi tuyển sinh lớp 10 môn Anh Đắk Lắk 2024
Đề thi tuyển sinh lớp 10 môn Toán Đắk Lắk 2023
Đề thi môn Toán kỳ thi vào lớp 10 năm 2023 tại tỉnh Đắk Lắk sẽ được Đọc Tài Liệu cập nhật ngay khi môn thi kết thúc.
ĐỀ THI

ĐÁP ÁN THAM KHẢO





Câu 7.

Đề thi tuyển sinh lớp 10 môn Toán Đắk Lắk 2022
Đề thi

Đáp án
Câu 1

Câu 2

Câu 3

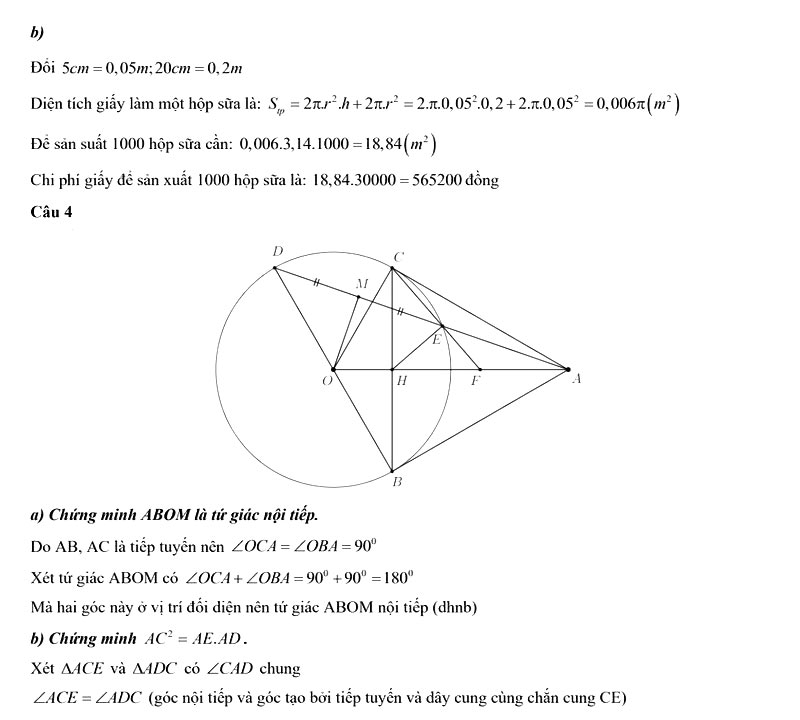
Câu 4

Câu 5

Tuyển tập đề thi vào 10 Đắk Lắk môn Toán các năm gần đây
Cùng ôn tập chuẩn bị thật tốt cho kỳ thi sắp tới với đề thi tuyển sinh lớp 10 các năm trước nhé:
Đề thi tuyển sinh lớp 10 môn Toán tỉnh Đắk Lắk năm 2021
Đề thi vào lớp 10 môn Toán tỉnh Đắk Lắk 2021 được cập nhật ngay sau thời gian làm bài ngày 09/06/2021.

Đáp án tham khảo
Câu 1.
1) \(2 x^{2}+5 x-3=0\)
Ta có \(\Delta=b^{2}-4 a c=(5)^{2}-4 *(2) *(-3)=49 >0 \)
Vậy phương trình đã cho có 2 nghiệm phân biệt.
\(\begin{aligned} &x_{1}=\frac{-b+\sqrt{\Delta}}{2 a}=\frac{-(5)+\sqrt{49}}{2 *(2)}=\frac{-5+\sqrt{49}}{4} = \dfrac{1}{2}\\ &x_{2}=\frac{-b-\sqrt{\Delta}}{2 a}=\frac{-(5)-\sqrt{49}}{2 *(2)}=\frac{-5-\sqrt{49}}{4} = -3 \end{aligned}\)
KL/. ...
2) Để hàm số y = (m-1) x + 2021 đồng biến trên ℝ thì m - 1 > 0 ⇔ m > 1.
KL: ... Vậy với ...
3)
\(\begin{aligned} &\text { Thay } a=1+\sqrt{2} \text { và } b=1-\sqrt{2} \text { vào } P=a+b-2 a b \text { ta được: }\\ &\begin{aligned} P &=1+\sqrt{2}+1-\sqrt{2}-2(1+\sqrt{2})(1-\sqrt{2}) \\ &=2-2\left[1-(\sqrt{2})^{2}\right] \\ &=2-2(1-2) \\ &=2+2=4 . \end{aligned}\\ &\text { Vậy } P=4 \text { khi } a=1+\sqrt{2} \text { và } b=1-\sqrt{2} \text { . } \end{aligned}\)
Câu 2.
1) \(\text { ĐKXD: } x \geq 0, x \neq 4, x \neq 9\)
\(\begin{aligned} P &=\frac{2 \sqrt{x}-9}{x-5 \sqrt{x}+6}-\frac{\sqrt{x}+3}{\sqrt{x}-2}+\frac{2 \sqrt{x}+1}{\sqrt{x}-3} \\ &=\frac{2 \sqrt{x}-9}{(\sqrt{x}-2)(\sqrt{x}-3)}-\frac{\sqrt{x}+3}{\sqrt{x}-2}+\frac{2 \sqrt{x}+1}{\sqrt{x}-3} \\ &=\frac{2 \sqrt{x}-9-(\sqrt{x}+3)(\sqrt{x}-3)+(2 \sqrt{x}+1)(\sqrt{x}-2)}{(\sqrt{x}-2)(\sqrt{x}-3)} \\ &=\frac{2 \sqrt{x}-9-(x-9)+(2 x-3 \sqrt{x}-2)}{(\sqrt{x}-2)(\sqrt{x}-3)} \\ &=\frac{2 \sqrt{x}-9-x+9+2 x-3 \sqrt{x}-2}{(\sqrt{x}-2)(\sqrt{x}-3)} \\ &=\frac{x-\sqrt{x}-2}{(\sqrt{x}-2)(\sqrt{x}-3)} \\ &=\frac{(\sqrt{x}+1)(\sqrt{x}-2)}{(\sqrt{x}-2)(\sqrt{x}-3)}=\frac{\sqrt{x}+1}{\sqrt{x}-3} \end{aligned}\)
KL: ...
2)
\(Điều kiện: x \geq 0, x \neq 4, x \neq 9\\ P>1 \Leftrightarrow \frac{\sqrt{x}+1}{\sqrt{x}-3}>1 \\ \Leftrightarrow \frac{\sqrt{x}+1}{\sqrt{x}-3}-1>0\\ \Leftrightarrow \frac{\sqrt{x}+1-(\sqrt{x}-3)}{\sqrt{x}-3}>0\\ \Leftrightarrow \frac{4}{\sqrt{x}-3}>0\\ \Leftrightarrow \sqrt{x}-3>0\,\,( do \,\,4>0)\\ \Leftrightarrow \sqrt{x}>3\\ \Leftrightarrow x>9\\\)
Kết hợp với điều kiện xác định ta được x > 9 thì P > 1
Vậy x > 9 thì P > 1.
Câu 3.

Câu 4.

Câu 5,
\(\begin{aligned} &\text { Ta có: } a^{2}+b^{2} \geq 2 a b \Leftrightarrow a^{2}+b^{2}+a b \geq 3 a b \\ &\left.\Rightarrow a^{2}+b^{2}+a b \geq \frac{3}{2} a b+\frac{3}{2} a b \geq \frac{3}{2} \cdot a \cdot 1348+\frac{3}{2} b .1348 \text { (Do } a \geq 1348, b \geq 1348\right) \\ &\Rightarrow a^{2}+b^{2}+a b \geq 2022(a+b)(đ p c m) \end{aligned}\)
Dấu "=" xảy ra khi a = b = 1348.
Đề thi tuyển sinh lớp 10 môn Toán Đắk Lắk năm 2020
Câu 2. (2,0 điểm) Cho biểu thức:
\(P=(\dfrac{1}{3+\sqrt{x}}+\dfrac{(\sqrt{x}+1)(\sqrt{x}+6)}{9-x}:\dfrac{2\sqrt{x}+1}{6-4\sqrt{x}}\)
- Tìm điều kiện của x để biểu thức P có nghĩa và rút gọn P.
- Tìm các giá trị của x sao cho \(\sqrt{x}\) và P là những số nguyên.
Xem chi tiết đề thi và đáp án tại link: Đề thi tuyển sinh lớp 10 môn Toán Đắk Lắk năm 2020
Đề thi tuyển sinh lớp 10 môn Toán Đắk Lắk năm 2019
Câu 1. (2,0 điểm)
- Rút gọn biểu thức: \(A=\sqrt{32}-\sqrt{6}.\sqrt{3}+\dfrac{\sqrt{22}}{\sqrt{11}} \)
- Giải phương trình: \(x^2-2x=0\)
- Xác định hệ số a của hàm số \(y=ax^2\), biết đồ thị của hàm số đó đi qua điểm A(-3;1)
Xem chi tiết đề thi và đáp án tại link: Đề thi vào lớp 10 môn Toán tỉnh Đắk Lắk năm 2019 (có đáp án)
Đề thi tuyển sinh lớp 10 môn Toán Đắk Lắk năm 2018
Câu 1.
- Tìm x biết \(2\sqrt{x}=3\)
- Giải phương trình: \(43x^2-2018x+1975=0\)
- Cho hàm số \(y=(a+1)x^2.\) Tìm a để hàm số nghịch biết khi \(x<0\) và đồng biết khi \(x>0\)
Xem chi tiết đề thi và đáp án tại link: Đáp án Toán thi vào lớp 10 tỉnh Đắk Lắk 2018
Trên đây là toàn bộ nội dung của đề thi tuyển sinh lớp 10 môn Toán 2023 và các năm trước tỉnh Đắk Lắk mà Đọc Tài Liệu chia sẻ nhằm giúp các em nắm được các thông tin về kỳ thi này.
Mong rằng những tài liệu của chúng tôi sẽ là người đồng hành giúp các bạn hoàn thành tốt bài thi của mình.
