Bạn đang tìm kiếm tài liệu tổng hợp kiến thức về các trường hợp đồng dạng của tam giác? Hãy tham khảo ngay bài viết dưới đây của Đọc tài liệu với những lý thuyết các trường hợp đồng dạng của tam giác vuông cùng tổng hợp các dạng toán cơ bản thường gặp. Đây sẽ là tài liệu học tập hữu ích cho học sinh và đồng thời giúp các thầy cô có thêm tài liệu hay phục vụ việc dạy học.
Cùng tham khảo nhé!

I. Lý thuyết các trường hợp đồng dạng của tam giác vuông
Từ các trường hợp đồng dạng của tam giác đã học suy ra: Hai tam giác vuông đồng dạng nếu có một trong các điều kiện:
+ Một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia;
+ Hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia.
Định lý:
Trường hợp đồng dạng đặc biệt: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đồng dạng.
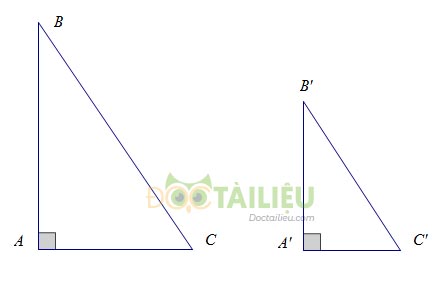
Nếu \(\Delta ABC\) và \(\Delta A'B'C'\) có \(\widehat A = \widehat {A'} = {90^o}\) và \(\dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}}\) (h.1) thì \(\Delta ABC\backsim\Delta A'B'C'\).
Tỉ số đường cao, tỉ số diện tích của hai tam giác đồng dạng
Nếu hai tam giác đồng dạng thì:
+ Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng;
+ Tỉ số hai diện tích bằng bình phương tỉ số đồng dạng.
II. Các dạng toán thường gặp các trường hợp đồng dạng của tam giác vuông
Dạng 1: Sử dụng tam giác đồng dạng , tỉ số đường cao, tỉ số diện tích để tính toán.
Phương pháp:
+ Từ tam giác đồng dạng suy ra các cặp cạnh tỉ lệ và các góc bằng nhau, suy ra tỉ số diện tích và tỉ số đường cao
+ Từ đó tính cạnh , góc và các dữ kiện cần thiết
Dạng 2: Chứng minh hai tam giác đồng dạng và các vấn đề liên quan.
Phương pháp:
+ Sử dụng các trường hợp đồng dạng của tam giác để chứng minh tam giác đồng dạng
+ Từ đó suy ra các hệ thức cần chứng minh
III. Bài tập mẫu về các trường hợp đồng dạng của tam giác vuông
Cho tam giác \(ABC\) vuông tại \(A\), \(;AC = 4cm, BC = 6cm.\) Kẻ tia \(Cx\) vuông góc với \(BC\) (tia \(Cx\) và điểm \(A \)khác phía so với đường thẳng \(BC\).Lấy trên tia \(Cx\) điểm \(D\) sao cho \(BD = 9cm\)
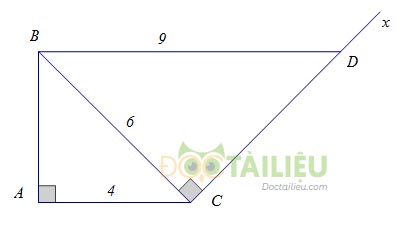
Chứng minh rằng \(BD // AC.\)
Lời giải:
\(\displaystyle {{AC} \over {CB}} = {4 \over 6} = {2 \over 3}\) \(\displaystyle{{CB} \over {BD}} = {6 \over 9} = {2 \over 3}\) \( \Rightarrow \displaystyle{{AC} \over {CB}} = {{CB} \over {BD}}\)
Xét hai tam giác vuông \(ABC\) và \(CDB\) có:
\(\widehat {BAC} = \widehat {DCB} = 90^\circ \)
\(\displaystyle {{AC} \over {CB}} = {{CB} \over {BD}}\) (chứng minh trên)
\( \Rightarrow ∆ ABC \backsim ∆ CDB\)(cạnh huyền và cạnh góc vuông tỉ lệ).
\( \Rightarrow \widehat {ACB} = \widehat {CBD}\)
Mà \(\widehat {ACB} \) và \( \widehat {CBD}\) ở vị trí so le trong nên \(AC // BD \).
=>> Xem thêm nhiều bài tập khác trong chuyên đề các trường hợp đồng dạng của tam giác vuông lớp 8 để củng cố kiến thức và rèn luyện kỹ năng làm bài
----------------------------
Trên đây là tổng hợp lý thuyết các trường hợp đồng dạng của tam giác vuông và các dạng bài thường gặp bao gồm các kiến thức cần nắm và cách làm các dạng bài tập liên quan mà Đọc tài liệu đã tổng hợp. Hy vọng đây sẽ là tài liệu học tập hữu ích cho các em học sinh cũng như các phụ huynh trong quá trình dạy học cho con em mình tại nhà. Ngoài ra đừng quên xem thêm những kiến thức khác và cách giải Toán 8 được cập nhật liên tục tại doctailieu.com. Chúc các em luôn học tốt và đạt kết quả cao!