Hệ thống kiến thức lý thuyết tiết vị trí tương đối của đường thẳng và đường tròn giúp các em nắm được kiến thức từ khái quát đến chi tiết để học tốt phần kiến thức này.
Mời các em cùng tham khảo:

I. Lý thuyết về vị trí tương đối của đường thẳng và đường tròn
1. Ba vị trí tương đối của đường thẳng và đường tròn
Cho đường tròn \(\left( {O;R} \right)\) và một đường thẳng \(a\) bất kì. Gọi d là khoảng cách từ tâm O của đường tròn đến đường thẳng đó.
a) Đường thẳng và đường tròn cắt nhau
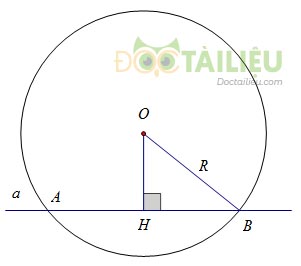
Khi đó, đường thẳng và đường tròn có hai điểm chung và khoảng cách d = OH \(<\) R
b) Đường thẳng và đường tròn tiếp xúc
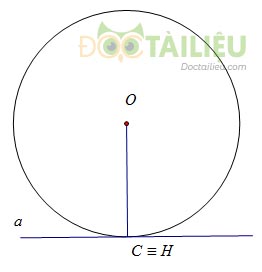
Khi đó, đường thẳng và đường tròn có một điểm chung và khoảng cách d = OB = R
Đường thẳng \(a\) được gọi là tiếp tuyến của đường tròn và điểm B là tiếp điểm.
c) Đường thẳng và đường tròn không giao nhau
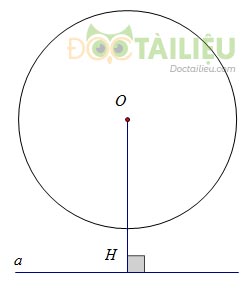
Khi đó, đường thẳng và đường tròn không có điểm chung và khoảng cách d = OH \(>\) R
Định lý:
Nếu một đường thẳng là tiếp tuyến của đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
2. Hệ thức giữa khoảng cách từ tâm đường tròn đến đường thẳng và bán kính của đường tròn
| Vị trí tương đối của đường thẳng và đường tròn | Số điểm chung | Hệ thức giữa \(d\) và \(R\) |
| Đường thẳng và đường tròn cắt nhau | 2 | \(d < R \) |
| Đường thẳng và đường tròn tiếp xúc | 1 | \(d = R\) |
| Đường thẳng và đường tròn không giao nhau | 0 | \(d > R\) |
II. Các dạng bài thường gặp về vị trí tương đối của đường thẳng và đường tròn
Dạng 1: Xác định vị trí tương đối của đường thẳng và đường tròn
Phương pháp: Dựa vào bảng vị trí tương đối :
Dạng 2: Bài toán độ dài dựa vào tính chất tiếp tuyến.
Phương pháp:
Sử dụng tính chất tiếp tuyến và định lý Pytago
Dạng 3: Tìm tập hợp điểm thỏa mãn điều kiện cho trước.
Phương pháp:
Sử dụng tính chất đường phân giác và các đường thẳng song song cách đều để tìm tập hợp điểm.
III. Bài tập về vị trí tương đối của đường thẳng và đường tròn
Cho điểm A cách đường thẳng xy là 12cm. Vẽ đường tròn (A ; 13cm).
a) Chứng minh rằng đường tròn (A) có hai giao điểm với đường thẳng xy.
b) Gọi hai giao điểm nói trên là B và C. Tính độ dài BC.
Lời giải:
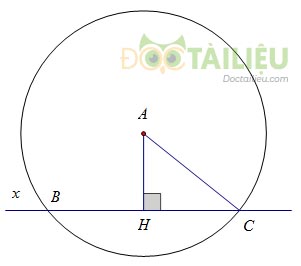
a) Kẻ AH \(⊥\) xy
Ta có: AH = 12cm
Bán kính đường tròn tâm I là 13cm nên R = 13cm.
Mà AH = d = 12cm
Nên suy ra d \(<\) R
Vậy ( A; 13cm) cắt đường thẳng xy tại hai điểm phân biệt B và C.
b) Áp dụng định lí Py-ta-go vào tam giác vuông AHC, ta có:
\(A{C^2} = A{H^2} + H{C^2}\)
Suy ra: \(H{C^2} = A{C^2} - A{H^2} = {13^2} - {12^2} = 25 \Rightarrow HC = 5(cm)\)
Ta có: \(BC = 2.HC = 2.5 = 10 (cm)\)
=>> Xem thêm nhiều bài tập khác trong chuyên đề toán hình 9 chương 2 bài 4 để củng cố kiến thức và rèn luyện kỹ năng làm bài
****************
Hy vọng với hệ thống kiến thức lý thuyết vị trí tương đối của đường thẳng và đường tròn trên đây, các em sẽ có thêm một tài liệu học tập hữu ích để học tốt hơn môn Toán 9. Chúc các em luôn học tốt và đạt kết quả cao!