Bạn đang tìm kiếm tài liệu tổng hợp kiến thức về bảng lượng giác? Hãy tham khảo ngay bài viết dưới đây của Đọc tài liệu với những lý thuyết bảng lượng giác cùng tổng hợp các dạng toán cơ bản thường gặp. Đây sẽ là tài liệu học tập hữu ích cho học sinh và đồng thời giúp các thầy cô có thêm tài liệu hay phục vụ việc dạy học.
Cùng tham khảo nhé!

I. Lý thuyết về bảng lượng giác
1. Cấu tạo của bảng lượng giác
- Bảng sin và côsin (Bảng VIII)
- Bảng tang và côtang (Bảng IX)
- Bảng tang của các góc gần \(90°\) (Bảng X)
Nhận xét:
2. Cách dùng bảng, dùng máy tính
a) Tìm tỉ số lượng giác của một góc nhọn cho trước.
b) Tìm số đo của góc nhọn khi biết một tỷ số lượng giác của góc đó.
II. Bài tập về bảng lượng giác
Cho hình:
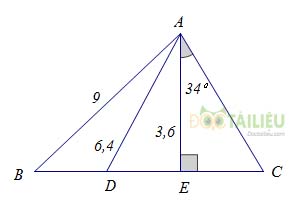
Biết:
\(AB = 9cm,AC = 6,4cm\)
\(AN = 3,6cm,\widehat {AN{\rm{D}}} = 90^\circ ,\widehat {DAN} = 34^\circ \)
Hãy tính:
a) \(CN\);
b) \(\widehat {ABN}\);
c) \(\widehat {CAN}\);
d) \(AD\).
Lời giải
a) Áp dụng định lí Pytago vào tam giác vuông ANC, ta có:
\( A{C^2} = A{N^2} + N{C^2} \Rightarrow N{C^2} = A{C^2} - A{N^2} \Rightarrow NC = \sqrt {A{C^2} - A{N^2}} = \sqrt {6,{4^2} - 3,{6^2}} = \sqrt {28} \Rightarrow NC = 5,2915\left( {cm} \right)\)
b) Tam giác ANB vuông tại N nên ta có:
\(\sin \widehat {ABN} = \dfrac{{AN}}{{AB}} = \dfrac{{3,6}}{ 9} = 0,4 \)
\( \Rightarrow \widehat {ABN} \approx 23^\circ 35'\)
c) Tam giác ANC vuông tại N nên ta có:
\(\eqalign{ & \cos \widehat {CAN} = {{AN} \over {AC}} \cr & = {{3,6} \over {6,4}} = {9 \over {16}} = 0,5625 \cr & \Rightarrow \widehat {CAN} \approx 55^\circ 46' \cr} \)
d) Tam giác AND vuông tại N nên ta có:
\(\eqalign{ & \cos \widehat {NAD} = {{AN} \over {AD}} \cr & \Rightarrow AD = {{AN} \over {\cos \widehat {NAD}}} \cr & = {{3,6} \over {\cos 34^\circ }} \approx 4,3424 \cr} \)
=>> Xem thêm nhiều bài tập khác trong chuyên đề Toán hình 9 chương 1 bài 3 để củng cố kiến thức và rèn luyện kỹ năng làm bài
*********************
Trên đây là lý thuyết bảng lượng giác bao gồm các kiến thức cần nắm và những dạng bài liên quan. Hy vọng đây sẽ là tài liệu hữu ích phục vụ việc học tập của các em. Ngoài ra, các em hãy truy cập doctailieu.com để tham khảo thêm nhiều tài liệu học Toán lớp 9 phong phú khác mà chúng tôi đã sưu tầm và tổng hợp nhé. Chúc các em luôn học tốt và đạt kết quả cao!