Trong chương trình Toán lớp 9, các em sẽ được làm quen với hệ thức lượng trong tam giác vuông. Đây là phần kiến thức quan trọng, những dạng toán về hệ thức lượng trong tam giác vuông sẽ xuất hiện trong hầu hết các bài thi quan trọng ở các mức độ khác nhau từ dễ đến khó.
Để các em nắm được đầy đủ kiến thức về phần này, Đọc Tài Liệu đem đến tài liệu tổng hợp lý thuyết chương 1 phần Hình học: Hệ thức lượng trong tam giác vuông ở bài viết dưới đây, hy vọng sẽ là một tài liệu hữu ích cho quá trình học tập của các em.
Cùng tham khảo nhé!

Tổng hợp kiến thức cần nắm chương 1 phần Hình học: Hệ thức lượng trong tam giác vuông
1. Hệ thức về cạnh và đường cao trong tam giác vuông
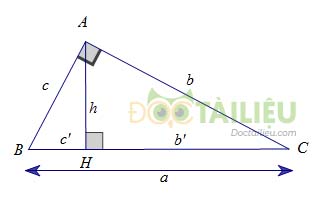
Cho tam giác \( ABC\) vuông tại \(A\), đường cao \(AH\). Khi đó ta có các hệ thức sau:
+) \( A{B^2} = BH.BC \) hay \({c^2} = a.c'\)
+) \( A{C^2} = CH.BC\) hay \({b^2} = ab'\)
+) \(AB.AC = BC.AH\) hay \( cb = ah\)
+) \(H{A^2} = HB.HC\) hay \({h^2} = c'b'\)
+) \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\).hay \(\dfrac{1}{{{h^2}}} = \dfrac{1}{{{c^2}}} + \dfrac{1}{{{b^2}}}\)
+) \(B{C^2} = A{B^2} + A{C^2}\) (Định lí Pitago).
2. Tỉ số lượng giác của góc nhọn
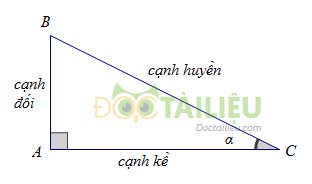
Các tỉ số lượng giác của góc nhọn \(\alpha\) (hình) được định nghĩa như sau:
\(\sin \alpha = \dfrac{{AB}}{{BC}};\cos \alpha = \dfrac{{AC}}{{BC}};\tan \alpha = \dfrac{{AB}}{{AC}};\cot \alpha = \dfrac{{AC}}{{AB}}\)
+ Nếu \(\alpha\) là một góc nhọn bất kỳ thì
\(0 < \sin \alpha < 1;0 < \cos \alpha < 1, \tan \alpha > 0;\cot \alpha > 0 , {\sin ^2}\alpha + {\cos ^2}\alpha = 1;\tan \alpha .\cot \alpha = 1\)
\(\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }};\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }};\)
\(1 + {\tan ^2}\alpha = \dfrac{1}{{{{\cos }^2}\alpha }};1 + {\cot ^2}\alpha = \dfrac{1}{{{{\sin }^2}\alpha }}\)
Chú ý: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Với hai góc \( \alpha ,\beta\) mà \(\alpha + \beta = {90^0}\),
Ta có: \(\sin \alpha = \cos \beta ;\cos \alpha = \sin \beta ;\tan \alpha = \cot \beta ;\cot \alpha = \tan \beta. \)
Nếu hai góc nhọn \(\alpha\) và \(\beta\) có \(\sin \alpha = \sin \beta\) hoặc \(\cos \alpha = \cos \beta\) thì \(\alpha = \beta\)
So sánh các tỉ số lượng giác
Với \( \alpha ,\beta\) là hai góc nhọn bất kì và \(\alpha < \beta\) thì
\(\sin \alpha < \sin \beta ;\,\cos \alpha > \cos \beta ;\tan \alpha < \tan \beta ;\cot \alpha > \cot \beta .\)
3. Bảng tỉ số lượng giác các góc đặc biệt
| 0⁰ | 30⁰ | 45⁰ | 60⁰ | 90⁰ | |
| sin α | 0 | \({1 \over 2} \) | \({√2 \over 2} \) | \({√3 \over 2} \) | 1 |
| cos α | 1 | \({√3 \over 2} \) | \({√2 \over 2} \) | \({1 \over 2} \) | 0 |
| tan α | 0 | \({√3 \over 3} \) | 1 | \(√3 \) | - |
| cot α | - | \(√3 \) | 1 | \({1 \over √3} \) | 0 |
4. Hệ thức về cạnh và góc trong tam giác vuông
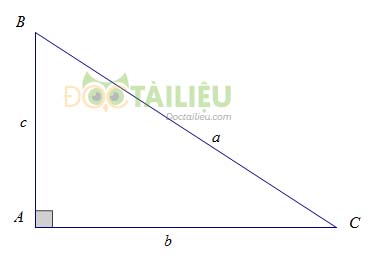
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = a,AC = b,AB = c\). Ta có :
\(b = a.\sin B = a.\cos C; c = a.\sin C = a.\cos B; b = c.\tan B = c.\cot C; c = b.\tan C = b.\cot B.\)
Trong một tam giác vuông
+) Cạnh góc vuông = (cạnh huyền ) x (sin góc đối) = (cạnh huyền ) x (cosin góc kề)
+) Cạnh góc vuông = (cạnh góc vuông ) x (tan góc đối) = (cạnh góc vuông còn lại ) x (cotan góc kề).
*******************
Hy vọng với hệ thống kiến thức lý thuyết chương 1 phần Hình học: Hệ thức lượng trong tam giác vuông trên đây, các em sẽ có thêm một tài liệu học tập hữu ích để học tốt hơn môn Toán 9. Chúc các em luôn học tốt và đạt kết quả cao!