Mời các em tham khảo tổng hợp lý thuyết sự xác định đường tròn - tính chất đối xứng của đường tròn cùng một số dạng bài thường gặp và hướng dẫn cách làm, qua đó nắm được các định lý, công thức và áp dụng hoàn thành các bài tập.

I. Lý thuyết về sự xác định đường tròn - tính chất đối xứng của đường tròn
a. Đường tròn
Tập hợp các điểm cách điểm \(O\) cố định một khoảng bằng R không đổi \(\left( {R > 0} \right)\) là đường tròn tâm \(O\) có bán kính \(R\). Kí hiệu: \(\left( O \right)\) hoặc \(\left( {O;R} \right)\).
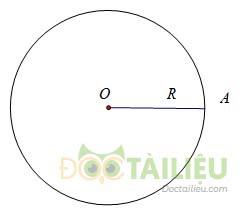
b. Vị trí tương đối của điểm M và đường tròn (O; R)
Nếu \(A\) nằm trên đường tròn \((O;R)\) thì \(OA=R\)
Nếu \(A\) nằm trong đường tròn \((O;R)\) thì \(OA<>
Nếu \(A\) nằm ngoài đường tròn \((O;R)\) thì \(OA>R\).
c. Định lý (về sự xác định một đường tròn)
- Qua ba điểm không thẳng hàng ta vẽ được một và chỉ một đường tròn.
- Đường tròn đi qua ba đỉnh của một tam giác gọi là đường tròn ngoại tiếp tam giác. Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó.
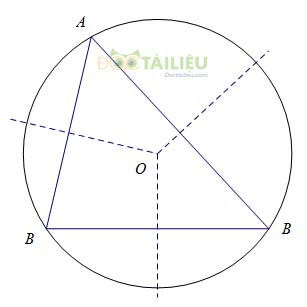
d. Tính chất đối xứng của đường tròn
+) Đường tròn là hình có tâm đối xứng. Tâm đường tròn là tâm đối xứng của đường tròn đó.
+) Đường tròn là hình có trục đối xứng. Bất kỳ đường kính nào cũng là trục đối xứng của đường tròn.
* Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp.
* Trong tam giác đều , tâm đường tròn ngoại tiếp là trọng tâm tam giác đó.
II. Các dạng toán thường gặp về sự xác định đường tròn - tính chất đối xứng của đường tròn
Dạng 1: Chứng minh các điểm cho trước cùng thuộc một đường tròn.
Phương pháp:
Chứng minh các điểm cho trước cùng cách đều một điểm nào đó. Điểm đó chính là tâm của đường tròn
Dạng 2: Xác định vị trí tương đối của một điểm đối với một đường tròn
Phương pháp:
Để xác định vị trí của điểm \(M\) đối với đường tròn \(\left( {O;R} \right)\) ta so sánh khoảng cách \(OM\) với bán kính \(R\):
Nếu \(A\) nằm trên đường tròn \((O;R)\) thì \(OA=R\)
Nếu \(A\) nằm trong đường tròn \((O;R)\) thì \(OA<>
Nếu \(A\) nằm ngoài đường tròn \((O;R)\) thì \(OA>R\).
Dạng 3: Xác định tâm và tính bán kính đường tròn ngoại tiếp
Phương pháp:
Ta thường sử dụng các kiến thức
- Sử dụng tính chất đường trung tuyến trong tam giác vuông.
- Dùng định lý Pytago.
- Dùng hệ thức lượng về cạnh và góc trong tam giác vuông.
III. Bài tập về sự xác định đường tròn - tính chất đối xứng của đường tròn
Cho tam giác đều ABC cạnh bằng 3cm. Bán kính của đường tròn ngoại tiếp tam giác ABC bằng:
(A) \(\,2\sqrt 3 \,cm\);
(B) 2cm;
(C) \(\,\sqrt 3 \,\)cm;
(D) \(\,\sqrt 2 \,\) cm;
Hãy chọn câu trả lời đúng.
Lời giải
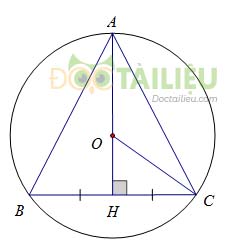
Vì O là tâm của đường tròn ngoại tiếp tam giác ABC nên O là giao điểm của ba đường trung trực trong tam giác ABC.
Kẻ \(AH \bot BC\), ta có: \(O \in AH\).
Trong tam giác vuông \(ABH\), ta có:
\(AH = AB.\sin \widehat B = 3.\sin 60^\circ = \dfrac{{3\sqrt 3 }}{ 2}\)
Vì tam giác ABC đều nên AH là đường cao cũng đồng thời là trung tuyến nên:
\(OA = \dfrac{2}{3}AH = \dfrac{2}{3}.\dfrac{{3\sqrt 3 }}{2} = \sqrt 3 \)
Vậy chọn đáp án C.
=>> Xem thêm nhiều bài tập khác trong chuyên đề toán hình 9 chương 2 bài 1 để củng cố kiến thức và rèn luyện kỹ năng làm bài
----------------------------
Trên đây là tổng hợp lý thuyết sự xác định đường tròn - tính chất đối xứng của đường tròn và các dạng bài thường gặp bao gồm các kiến thức cần nắm và cách làm các dạng bài tập liên quan mà Đọc tài liệu đã tổng hợp. Ngoài ra đừng quên xem thêm những kiến thức khác và cách giải Toán 9 được cập nhật liên tục tại doctailieu.com. Chúc các em luôn học tốt và đạt kết quả cao!