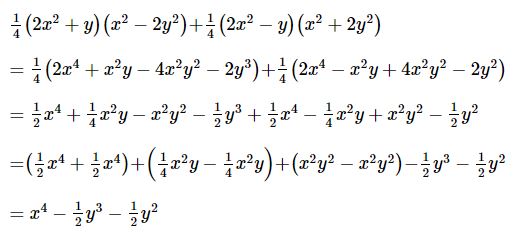Hướng dẫn trả lời câu hỏi và giải bài tập Toán 8 Kết nối tri thức tập 1 giúp học sinh nắm được các cách giải bài tập Chương 1: Đa thức chuẩn bị bài trước khi tới lớp và luyện tập giải toán tại nhà.
Bài tập cuối chương 1
Trắc nghiệm
Bài 1.39 trang 27 Toán 8 Tập 1: Đơn thức \(−23x^2yz^3\) có
A. hệ số −2, bậc 8.
B. hệ số −23, bậc 5.
C. hệ số −1, bậc 9.
D. hệ số −23, bậc 6.
Lời giải:
Đáp án đúng là: D
Đơn thức \(−23x^2yz^3\) có hệ số là −23 và có bậc là: 2 + 1 + 3 = 6.
Vậy đơn thức \(−23x^2yz^3 \)có hệ số là −23 và có bậc là 6.
Bài 1.40 trang 27 Toán 8 Tập 1: Gọi T là tổng, H là hiệu của hai đa thức \(3x^2y – 2xy^2 + xy và –2x^2y + 3xy^2 + 1\). Khi đó:
A. \(T = x^2y – xy^2 + xy + 1\) và \(H = 5x^2y – 5xy^2 + xy – 1\).
B. \(T = x^2y + xy^2 + xy + 1\) và \(H = 5x^2y – 5xy^2 + xy – 1\).
C. \(T = x^2y + xy^2 + xy + 1\) và \(H = 5x^2y – 5xy^2 – xy – 1\).
D. \(T = x^2y + xy^2 + xy – 1\) và \(H = 5x^2y + 5xy^2 + xy – 1\).
Lời giải:
Đáp án đúng là: B
Ta có:
• \(T = (3x^2y – 2xy^2 + xy) + (–2x^2y + 3xy^2 + 1)\)
\(= 3x^2y – 2xy^2 + xy – 2x^2y + 3xy^2 + 1\)
\(= (3x^2y – 2x^2y) + (3xy^2 – 2xy^2) + xy + 1\)
\(= x^2y + xy^2 + xy + 1\).
• \(H = (3x^2y – 2xy^2 + xy) – (–2x^2y + 3xy^2 + 1)\)
\(= 3x^2y – 2xy^2 + xy + 2x^2y – 3xy^2 – 1\)
\(= (3x^2y + 2x^2y) – (3xy^2 + 2xy^2) + xy – 1\)
\(= 5x^2y – 5xy^2 + xy – 1\).
Vậy \(T = x^2y + xy^2 + xy + 1; H = 5x^2y – 5xy^2 + xy – 1\).
Bài 1.41 trang 27 Toán 8 Tập 1: Tích của hai đơn thức \(6x^2yz\) và \(−2y^2z^2\) là đơn thức
A. \(4x^2y^3z^3\).
B. \(−12x^2y^3z^3\).
C. \(−12x^3y^3z^3\).
D. \(4x^3y^3z^3\).
Lời giải:
Đáp án đúng là: B
Ta có \(6x^2yz . (−2y^2z^2) = [6 . (−2)] x^2 (y . y^2) (z . z^2) = −12x^2y^3z^3\).
Vậy tích của hai đơn thức \(6x^2yz\) và \(−2y^2z^2\) là đơn thức \(−12x^2y^3z^3\).
Bài 1.42 trang 27 Toán 8 Tập 1: Khi chia đa thức \(8x^3y^2 – 6x^2y^3\) cho đơn thức −2xy, ta được kết quả là
A. \(−4x^2y + 3xy^2\).
B. \(−4xy^2 + 3x^2y\).
C. \(−10x^2y + 4xy^2\).
D. \(−10x^2y + 4xy^2\).
Lời giải:
Đáp án đúng là: A
Ta có \((8x^3y^2 – 6x^2y^3) : (−2xy) = 8x^3y^2 : (−2xy) – 6x^2y^3 : (−2xy)\)
\(= −4x^2y + 3xy^2\).
Vậy khi chia đa thức \(8x^3y^2 – 6x^2y^3\) cho đơn thức −2xy, ta được kết quả là \(−4x^2y + 3xy^2\).
Tự luận
Bài 1.43 trang 27 Toán 8 Tập 1: Một đa thức hai biến bậc hai thu gọn có thể nhiều nhất
a) bao nhiêu hạng tử bậc hai? Cho ví dụ.
b) bao nhiêu hạng tử bậc nhất? Cho ví dụ.
c) bao nhiêu hạng tử khác 0? Cho ví dụ.
Lời giải:
a) Một đa thức hai biến bậc hai thu gọn có thể nhiều nhất 3 hạng tử bậc hai.
Ví dụ: \(2x^2 – y^2 + 4xy + 5\); đa thức này có 3 hạng tử bậc hai là \(2x^2\); \(y^2\) và 4xy.
b) Một đa thức hai biến bậc hai thu gọn có thể nhiều nhất 2 hạng tử bậc nhất.
Ví dụ: \(2x+5y-\dfrac{1}{6}\); đa thức này có 2 hạng tử bậc nhất là 2x và 5y.
c) Bổ sung sau.
Bài 1.44 trang 27 Toán 8 Tập 1: Cho biểu thức \(3x^3(x^5 – y^5) + y^5(3x^3 – y^3)\).
a) Rút gọn biểu thức đã cho.
b) Tính giá trị của biểu thức đã cho nếu biết \(y^4 = x^4\sqrt{3}\)
Lời giải:
a) Ta có \(3x^3(x^5 – y^5) + y^5(3x^3 – y^3)\)
\(= 3x^3 . x^5 – 3x^3 . y^5 + y^5 . 3x^3 – y^5 . y^3\)
\(= 3x^8 – 3x^3y^5 + 3x^3y^5 – y^8 = 3x^8 – y^8\).
b) Ta có \(y^4 = x^4\sqrt{3}\) suy ra \((y^4)^2 = (x^4\sqrt{3})^2\) hay \(y^8 = 3x^8\)
Thay \(y^8 = 3x^8\) vào biểu thức \(3x^8 – y^8\), ta được: \(3x^8 – 3x^8 = 0\).
Vậy nếu \(y^4 = x^4\sqrt{3}\) thì giá trị của biểu thức đã cho bằng 0.
Bài 1.45 trang 28 Toán 8 Tập 1: Rút gọn biểu thức:
\(\dfrac{1}{4}(2x^2+y)(x^2-2y^2)+\dfrac{1}{4}(2x^2-y)(x^2+2y^2)\)
Lời giải:
Bài 1.46 trang 28 Toán 8 Tập 1: Bạn Thành dùng một miếng bìa hình chữ nhật để làm một chiếc hộp (không nắp) bằng cách cắt bốn hình vuông cạnh x centimét ở bốn góc (H.1.3) rồi gấp lại. Biết rằng miếng bìa có chiều dài là y centimét, chiều rộng là z centimét.
Tìm đa thức (ba biến x, y, z) biểu thị thể tích của chiếc hộp. Xác định bậc của đa thức đó.
Lời giải:
Cắt miếng bìa hình chữ nhật để làm một chiếc hộp (không nắp) thì chiếc hộp có:
- Chiều dài của đáy chiếc hộp là: y – 2x (cm)
- Chiều rộng của đáy chiếc hộp là: z – 2x (cm)
- Chiều rộng của chiếc hộp là x (cm)
Đa thức biểu thị thể tích của chiếc hộp là:
\(x(y – 2x)(z – 2x) = (xy – 2x2)(z – 2x) = xyz – 2x^2y – 2x^2z + 4x^3\)
.Đa thức \(xyz – 2x^2y – 2x^2z + 4x^3\) có bậc là 3.
Bài 1.47 trang 28 Toán 8 Tập 1: Biết rằng D là một đơn thức sao cho \(–2x^3y^4 : D = xy^2\). Hãy tìm thương của phép chia:
\((10x^5y^2 – 6x^3y^4 + 8x^2y^5) : D\).
Lời giải:
Ta có \(–2x^3y^4 : D = xy^2\).
Suy ra \(D = –2x^3y^4 : xy^2 = –2x^2y^2\).
Khi đó, \((10x^5y^2 – 6x^3y^4 + 8x^2y^5) : D\)
\(= (10x^5y^2 – 6x^3y^4 + 8x^2y^5) : (–2x^2y^2)\)
\(= 10x^5y^2 : (–2x^2y^2) – 6x^3y^4 : (–2x^2y^2) + 8x^2y^5 : (–2x^2y^2)\)
\(= –5x^3 + 3xy^2 – 4y^3\).
Vậy \((10x^5y^2 – 6x^3y^4 + 8x^2y^5) : D = –5x^3 + 3xy^2 – 4y^3\).
Bài 1.48 trang 28 Toán 8 Tập 1: Làm phép chia sau theo hướng dẫn:
\([8x^3(2x – 5)^2 – 6x^2(2x – 5)^3 + 10x(2x – 5)^2] : 2x(2x – 5)^2\).
Hướng dẫn: Đặt y = 2x – 5.
Lời giải:
Đặt y = 2x – 5.
Khi đó, ta có \([8x^3(2x – 5)^2 – 6x^2(2x – 5)^3 + 10x(2x – 5)^2] : 2x(2x – 5)^2\)
\(= (8x^3y^2 – 6x^2y^3 + 10xy^2) : 2xy^2\)
\(= 8x^3y^2 : 2xy^2 – 6x^2y^3 : 2xy^2 + 10xy^2 : 2xy^2\)
\(= 4x^2 – 3xy + 5 = 4x^2 – 3x(2x – 5) + 5\)
\(= 4x^2 – 6x^2 + 15x + 5 = – 2x^2 + 15x + 5\).
Vậy \([8x^3(2x – 5)^2 – 6x^2(2x – 5)^3 + 10x(2x – 5)^2] : 2x(2x – 5)^2 = – 2x^2 + 15x + 5\).
-//-
Hy vọng với nội dung trả lời chi tiết câu hỏi trong Bài tập cuối chương 1 giúp học sinh nắm được nội dung bài học và ghi nhớ những nội dung chính, quan trọng trong chương trình học Toán học 8.