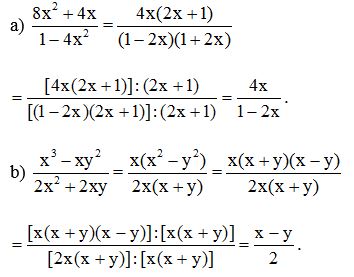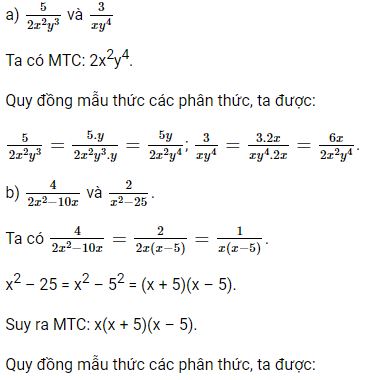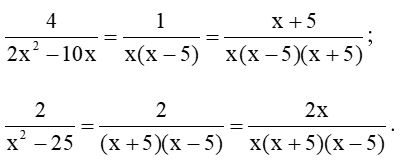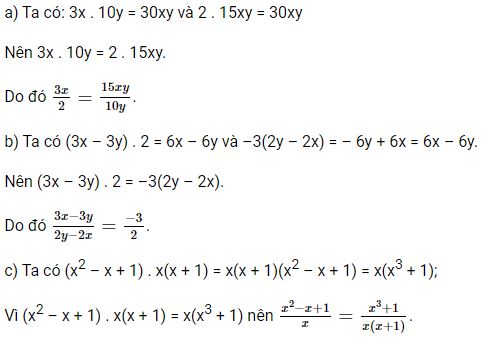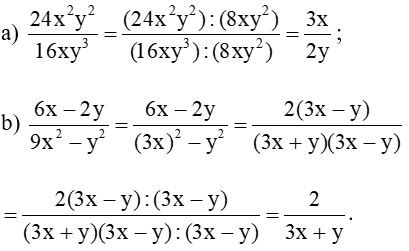Hướng dẫn trả lời câu hỏi và giải bài tập Toán 8 Cánh Diều tập 1 giúp học sinh nắm được các cách giải bài tập Chương 2: Phân thức đại số chuẩn bị bài trước khi tới lớp và luyện tập giải toán tại nhà.
Chương 2 Bài 1: Phân thức đại số
Khởi động trang 29 Toán 8 Tập 1: Ở lớp 6, ta đã biết kết quả của phép chia số nguyên a cho số nguyên b khác 0 có thể viết dưới dạng \(\dfrac{a}{b}\), ta gọi \(\dfrac{a}{b}\) là phân số. Tương tự, kết quả của phép chia đa thức P cho đa thức Q khác đa thức 0 cũng có thể viết dưới dạng \(\dfrac{P}{Q}\). Khi đó, biểu thức \(\dfrac{P}{Q}\) được gọi là gì?
Lời giải:
Kết quả của phép chia đa thức P cho đa thức Q khác đa thức 0 cũng có thể viết dưới dạng \(\dfrac{P}{Q}\). Khi đó, biểu thức \(\dfrac{P}{Q}\) được gọi là phân thức.
Hoạt động 1 trang 29 Toán 8 Tập 1: Cho biểu thức \(\dfrac{2x+1}{x-2}\)
a) Biểu thức 2x + 1 có phải đa thức hay không?
b) Biểu thức x – 2 có phải đa thức khác đa thức 0 hay không?
Lời giải:
a) Biểu thức 2x + 1 là đa thức.
a) Biểu thức x – 2 là đa thức khác đa thức 0.
Luyện tập 1 trang 30 Toán 8 Tập 1: Trong những biểu thức sau, biểu thức nào là phân thức?
a) \(\dfrac{x^2y+xy^2}{x-y}\)
b) \(\dfrac{x^2-1}{\dfrac{1}{x}}\)
Lời giải:
a) Do x2y + xy2 và x – y là các đa thức và đa thức x – y khác đa thức 0 nên biểu thức \(\dfrac{x^2y+xy^2}{x-y}\) là phân thức.
b) Do biểu thức \(\dfrac{1}{x}\) không phải là các đa thức nên biểu thức \(\dfrac{x^2-1}{\dfrac{1}{x}}\) không phải là phân thức.
Hoạt động 2 trang 30 Toán 8 Tập 1: Cho hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\). Nêu quy tắc để hai phân số bằng nhau.
Lời giải:
Quy tắc để hai phân số bằng nhau là:
Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) được gọi là bằng nhau nếu a . d = b . c, viết là \(\dfrac{a}{b}\) = \(\dfrac{c}{d}\)
Luyện tập 2 trang 30 Toán 8 Tập 1: Mỗi cặp phân thức sau có bằng nhau không? Vì sao?
a) \(\dfrac{x+y}{x^2-y^2}\) và \(\dfrac{1}{x-y}\)
b) \(\dfrac{x}{x^2-1}\) và \(\dfrac{1}{x-1}\)
Lời giải:
a) Ta có: \((x + y)(x – y) = x^2 – y^2\) và \((x^2 – y^2) . 1 = x^2 – y^2\).
Nên \((x + y)(x – y) = (x^2 – y^2) . 1\).
Vậy \(\dfrac{x+y}{x^2-y^2} = \dfrac{1}{x-y}\)
b) Ta có: \(x(x – 1) = x^2 – x\) và \((x^2 – 1) . 1 = x^2 – 1\)
Do \(x(x – 1) ≠ (x^2 – 1) . 1\) nên hai phân thức \(\dfrac{x}{x^2-1}\) và \(\dfrac{1}{x-1}\) không bằng nhau.
Luyện tập 3 trang 32 Toán 8 Tập 1: Dùng tính chất cơ bản của phân thức, hãy giải thích vì sao có thể viết: \(\dfrac{3x+y}{y} = \dfrac{3xy+y^2}{y^2}\)
Lời giải:
Nhân cả tử và mẫu của phân thức đã cho với y, ta được:
\(\dfrac{3x+y}{y} = \dfrac{(3x+y)y}{y.y} = \dfrac{3xy+y^2}{y^2}\) (theo tính chất cơ bản của phân thức).
Hoạt động 4 trang 32 Toán 8 Tập 1: Cho phân thức \(\dfrac{4x^2y}{6xy^2}\)
a) Tìm nhân tử chung của tử và mẫu.
b) Tìm phân thức nhận được sau khi chia cả tử và mẫu cho nhân tử chung đó.
Lời giải:
a) Nhân tử chung của tử và mẫu là 2xy.
b) Ta có: \(\dfrac{4x^2y}{6xy^2} = \dfrac{4x^{2y}:2xy}{6xy^2:2xy} = \dfrac{2x}{3y}\)
Vậy sau khi chia cả tử và mẫu cho nhân tử chung thì phân thức nhận được là \(\dfrac{2x}{3y}\)
Luyện tập 4 trang 32 Toán 8 Tập 1: Rút gọn mỗi phân thức sau:
a) \(\dfrac{8x^2+4x}{1-4x^2}\);
b) \(\dfrac{x^3 - xy^2}{2x^2+2xy}\).
Lời giải:
Hoạt động 5 trang 33 Toán 8 Tập 1: Cho hai phân thức \(\dfrac{1}{x^2y}\) và \(\dfrac{1}{xy^2}\)
a) Hãy nhân cả tử và mẫu của phân thức thứ nhất với y và nhân cả tử và mẫu của phân thức thứ hai với x.
b) Nhận xét gì về mẫu của hai phân thức thu được.
Lời giải:
Hoạt động 6 trang 33 Toán 8 Tập 1: Tìm MTC của hai phân thức \(\dfrac{5}{2x+6}\) và \(\dfrac{3}{x^2-9}\).
Lời giải:
Để tìm MTC của hai phân thức trên, ta có thể làm như sau:
Bước 1. Phân tích mẫu của mỗi phân thức đã cho thành nhân tử
2x + 6 = 2(x + 3); x2 – 9 = (x – 3)(x + 3).
Bước 2. Chọn MTC là: 2(x – 3)(x + 3).
Cách tìm mẫu thức như bảng sau:
| Nhân tử bằng số | Lũy thừa của x – 3 | Lũy thừa của x + 3 | |
|---|---|---|---|
| Mẫu thức 2x + 6 = 2(x + 3) | 2 | x + 3 | |
| Mẫu thức | 1 | x – 3 | x + 3 |
| MTC 2(x – 3)(x + 3) | 2 = BCNN(2, 1) | x – 3 | x + 3 |
Hoạt động 7 trang 33 Toán 8 Tập 1: Quy đồng mẫu thức hai phân thức \(\dfrac{1}{x^2+x}\) và \(\dfrac{1}{x^2-x}\)
Lời giải:
Luyện tập 5 trang 34 Toán 8 Tập 1: Quy đồng mẫu thức các phân thức trong mỗi trường hợp sau:
a) \(\dfrac{5}{2x^2y^3}\) và \(\dfrac{3}{xy^4}\);
b) \(\dfrac{4}{2x^2-10x}\) và \(\dfrac{2}{x^2-25}\).
Lời giải:
Hoạt động 8 trang 34 Toán 8 Tập 1: Cho phân thức \(\dfrac{2x^2-x+1}{x-2}\). Tìm giá trị của x sao cho mẫu x – 2 ≠ 0.
Lời giải:
Để mẫu x – 2 ≠ 0 thì x≠ 2.
Vậy giá trị của x sao cho mẫu x – 2 ≠ 0 là x≠ 2.
Bài 1 trang 37 Toán 8 Tập 1: Viết điều kiện xác định của mỗi phân thức sau:
a) \(\dfrac{y}{3y+3}\);
b) \(\dfrac{4x}{x^2+16}\);
c) \(\dfrac{x+y}{x-y}\)
Lời giải:
a) Điều kiện xác định của phân thức \(\dfrac{y}{3y+3}\) là 3y + 3 ≠ 0;
b) Điều kiện xác định của phân thức \(\dfrac{4x}{x^2+16}\) là x2 + 16 ≠ 0;
c) Điều kiện xác định của phân thức \(\dfrac{x+y}{x-y}\) là x – y ≠ 0.
Bài 2 trang 37 Toán 8 Tập 1: Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng:
a) \(\dfrac{3x}{2} = \dfrac{15xy}{10y}\);
b) \(\dfrac{3x-3y}{2y-2x} = \dfrac{-3}{2}\);
c) \(\dfrac{x^2-x+1}{x} = \dfrac{x^3+1}{x(x+1)}\)
Lời giải:
Bài 3 trang 37 Toán 8 Tập 1: Rút gọn mỗi phân thức sau:
a) \(\dfrac{24x^2y^2}{16xy^3}\);
b) \(\dfrac{6x-2y}{9x^2-y^2}\).
Lời giải:
Bài 4 trang 37 Toán 8 Tập 1: Quy đồng mẫu thức các phân thức trong mỗi trường hợp sau:
a) \(\dfrac{2}{x-3y} và \dfrac{3}{x+3y}\);
b) \(\dfrac{7}{4x+24} và \dfrac{13}{x^2-36}\).
Lời giải:
Bài 5 trang 37 Toán 8 Tập 1: Cho hình chữ nhật ABCD và MNPQ như Hình 1 (các số đo trên hình tính theo đơn vị centimét).
a) Viết phân thức biểu thị tỉ số diện tích của hình chữ nhật ABCD và hình chữ nhật MNPQ.
b) Tính giá trị của phân thức đó tại x = 2 và tại x = 5.
Lời giải:
Bài 6 trang 37 Toán 8 Tập 1: Chị Hà mở một xưởng thủ công với vốn đầu tư ban đầu (xây dựng nhà xưởng, mua máy móc, ...) là 80 triệu. Biết chi phí để sản xuất (tiền mua vật liệu, lương công nhân) của 1 sản phẩm là 15 nghìn đồng. Gọi x là số sản phẩm mà xưởng của chị Hà làm được.
a) Viết phân thức biểu thị số tiền thực (đơn vị nghìn đồng) đã bỏ ra để làm được x sản phẩm.
b) Viết phân thức biểu thị chi phí thực (đơn vị nghìn đồng) để tạo ra 1 sản phẩm theo x.
c) Tính chi phí thực để tạo ra 1 sản phẩm nếu x = 100; x = 1 000. Nhận xét về chi phí thực để tạo ra 1 sản phẩm nếu x ngày càng tăng.
Lời giải:
-//-
Hy vọng với nội dung trả lời chi tiết câu hỏi trong Bài 1: Phân thức đại số giúp học sinh nắm được nội dung bài học và ghi nhớ những nội dung chính, quan trọng trong chương trình học Toán học 8.