Bài 1 trang 9 SGK Giải tích 12

Bài 1: Xét sự đồng biến, nghịch biến của các hàm số

a) \(y = 4 + 3x - x^2\)      b) \(y ={1 \over 3}x^3\) + \(3x^2-7x - 2\) 
c) \(y = x^4\) - \(2x^2\) +\( 3\)       d) \(y = -x^3\)+ \(x^2\) - \(5\).

Hướng dẫn giải bài 1 trang 9 SGK Giải tích 12

- Tìm tập xác định của hàm số.

- Tính đạo hàm của hàm số. Tìm các điểm xi (I =1,2,3,…,n) mà tại đó đạo hàm bằng 0 hoặc không xác định

- Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên

- Dựa vào bảng biến thiên để kết luận khoảng đồng biến và nghịch biến của hàm số trên tập xác định của nó. (nếu y’ > 0 thì hàm số đồng biến, nếu y’ < 0 thì hàm số nghịch biến)

Chú ý: Khi kết luận các khoảng đồng biến và nghịch biến của hàm số ta nhớ sử dụng chữ và chứ không được sử dụng kí hiệu hợp.

Để xét xem dấu của hàm số là + hay - trong một khoảng nào đó ở bảng biến thiên, bạn lấy một giá trị bất kì nằm trong khoảng đó, thay vào đạo hàm y'. Nếu y' là dương thì dấu của y' trong khoảng đó là + và ngược lại.

Ví dụ: xét dấu y' = -x2 + 4 trong khoảng (-2; 2). Chẳng hạn ta lấy một giá trị bất kì trong khoảng là 1, thay vào y' ta được: y' = -(-1)2 + 4 = 3 > 0. Do đó dấu của y' trong khoảng (-2; 2) sẽ là +.)

Lời giải và đáp án bài 1 trang 9 SGK Giải tích 12

a) \(y=4+3x-{{x}^{2}}\)

Tập xác định: \(D=R.\)Có \(y'=3-2x\Rightarrow y'=0\Leftrightarrow 3-2x=0\Leftrightarrow x=\frac{3}{2}.\)

Bảng biến thiên:

 
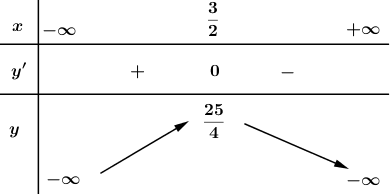
Vậy hàm số đồng biến trên khoảng \(\left( -\infty ;\frac{3}{2} \right)\)  và nghịch biến trên khoảng \(\left( \frac{3}{2};+\infty  \right).\)

b) \(y=\frac{1}{3}{{x}^{3}}+3{{x}^{2}}-7x-2\)

Tập xác định: \(D=R.\)

Có \(y'={{x}^{2}}+6x-7\Rightarrow y'=0\Leftrightarrow {{x}^{2}}+6x-7=0\Leftrightarrow \left[ \begin{align} & x=1 \\ & x=-7 \\ \end{align} \right..\)

Bảng biến thiên: 

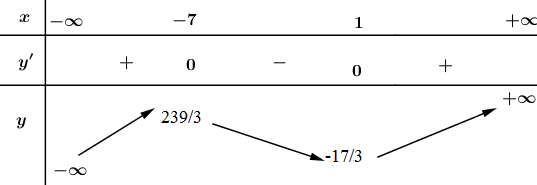
Vậy hàm số đồng biến trên các khoảng \(\left( -\infty ;-7 \right)\) và \(\left( 1;+\infty  \right)\).Hàm số nghịch biến trên \(\left( -7;\ 1 \right).\)

c) \(y={{x}^{4}}-2{{x}^{2}}+3\)   

Tập xác định: \(D=R.\)

Có \(y'=4{{x}^{3}}-4x\Rightarrow y'=0\Leftrightarrow 4{{x}^{3}}-4x=0\Leftrightarrow \left[ \begin{align}& x=-1 \\ & x=0 \\ & x=1 \\ \end{align} \right..\)

Bảng biến thiên:

 

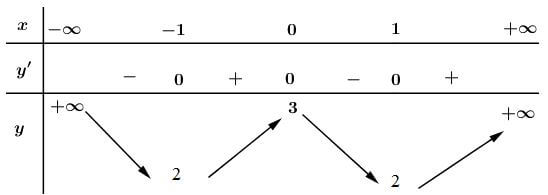
Vậy hàm số đồng biến trên các khoảng \(\left( -1;\ 0 \right)\) và \(\left( 1;+\infty  \right).\)Hàm số nghịch biến trên các khoảng \(\left( -\infty ;-1 \right)\) và \(\left( 0;\ 1 \right).\)

d) \(y=-{{x}^{3}}+{{x}^{2}}-5\)

Tập xác định: \(D=R.\)

Có \(y'=-3{{x}^{2}}+2x=0\Rightarrow y'=0\Leftrightarrow -3{{x}^{2}}+2x=0\Leftrightarrow \left[ \begin{align} & x=0 \\  & x=\frac{2}{3} \\ \end{align} \right..\)

Bảng biến thiên:

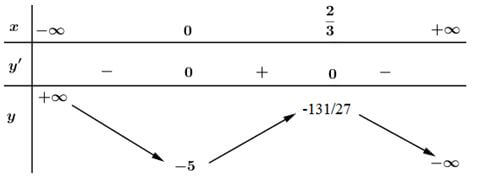
Vậy hàm số đồng biến trên khoảng \(\left( 0;\frac{2}{3} \right).\)Hàm số nghịch biến trên các khoảng \(\left( -\infty ;0 \right)\) và \(\left( \frac{2}{3};+\infty  \right).\)

» Xem đáp án bài tiếp theo: Bài 2 trang 10 SGK Giải tích 12

Trên đây là hướng dẫn giải bài 1 trang 9 SGK Giải tích 12, mời các bạn tham khảo thêm đáp án các bài tập về giải toán 12 bài 1 hoặc hướng dẫn chi tiết các bài tập Giải tích 12 khác tại doctailieu.com.