Bài 2 trang 10 SGK Giải tích 12

Đề bài : Bài 2 trang 10 SGK Giải tích 12 

Tìm các khoảng đơn điệu của các hàm số:

a)  \(y=\frac{3x+1}{1-x}\) ;                           b) \(y=\frac{x^{2}-2x}{1-x}\) ;

c) \(y=\sqrt{x^{2}-x-20}\) ;              d) \(y=\frac{2x}{x^{2}-9}\).

Hướng dẫn phương pháp giải chi tiết

- Tìm tập xác định của hàm số.

- Tính đạo hàm của hàm số. Tìm các điểm xi (I =1,2,3,…,n) mà tại đó đạo hàm bằng 0 hoặc không xác định

- Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên

- Dựa vào bảng biến thiên để kết luận khoảng đồng biến và nghịch biến của hàm số trên tập xác định của nó. (nếu y’ > 0 thì hàm số đồng biến, nếu y’ < 0 thì hàm số nghịch biến)

Cần chú ý các tập xác định của hàm số.

Đáp án bài 2 trang 10 SGK Giải Tích lớp 12

a) \(y=\frac{3x+1}{1-x}=\frac{3x+1}{-x+1}\)        

Tập xác định: \(D=R\backslash \left\{ 1 \right\}.\)

Có: \(y'=\frac{3.1-(-1).1}{{{\left( -x+1 \right)}^{2}}}=\frac{4}{{{\left( -x+1 \right)}^{2}}}>0\ \forall \ x\in D.\)

Bảng biến thiên:

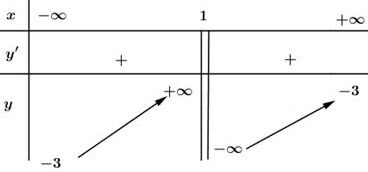
Vậy hàm số đồng biến trên các khoảng xác định của nó là: \(\left( -\infty ;\ 1 \right)\) và \(\left( 1;+\infty  \right).\)

* Chú ý cách tính giới hạn để điền vào bảng biến thiên:

\(\underset{x\to \pm \infty }{\mathop{\lim }}\,\frac{3x+1}{1-x}=-3;\ \ \underset{x\to {{1}^{+}}}{\mathop{\lim }}\,\frac{3x+1}{1-x}=-\infty ;\ \ \ \underset{x\to {{1}^{-}}}{\mathop{\lim }}\,\frac{3x+1}{1-x}=+\infty \)              

b) \(y=\frac{{{x}^{2}}-2x}{1-x}.\)

Tập xác định: \(D=R\backslash \left\{ 1 \right\}.\)

Có:

 \(\begin{align}& y'=\frac{\left( 2x-2 \right)\left( 1-x \right)+{{x}^{2}}-2x}{{{\left( 1-x \right)}^{2}}}=\frac{-{{x}^{2}}+2x-2}{{{\left( 1-x \right)}^{2}}}=\frac{-\left( {{x}^{2}}-2x+2 \right)}{{{\left( 1-x \right)}^{2}}}=\frac{-\left( {{x}^{2}}-2x+1 \right)-1}{{{\left( 1-x \right)}^{2}}} \\ & =\frac{-{{\left( x-1 \right)}^{2}}-1}{{{\left( 1-x \right)}^{2}}}=-1-\frac{1}{{{\left( 1-x \right)}^{2}}}<0\ \forall x\in D. \\ \end{align}\)

Bảng biến thiên:

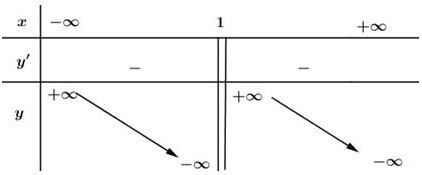
Vậy hàm số nghịch biến trên các khoảng xác định của nó là: \(\left( -\infty ;\ 1 \right)\) và \(\left( 1;+\infty  \right).\)           

Chú ý cách tính giới hạn để điền vào bảng biến thiên: Bài 2 trang 10 SGK Giải Tích lớp 12

\(\begin{align}& \underset{x\to +\infty }{\mathop{\lim }}\,\frac{{{x}^{2}}-2x}{1-x}=-\infty ;\ \ \ \ \ \underset{x\to -\infty }{\mathop{\lim }}\,\frac{{{x}^{2}}-2x}{1-x}=+\infty \  \\ & \underset{x\to {{1}^{+}}}{\mathop{\lim }}\,\frac{3x+1}{1-x}=+\infty ;\ \ \ \ \ \ \underset{x\to {{1}^{-}}}{\mathop{\lim }}\,\frac{3x+1}{1-x}=-\infty  \\ \end{align}\)

c) \(y=\sqrt{{{x}^{2}}-x-20}\)                     

Có \({{x}^{2}}-x-20\ge 0\Leftrightarrow \left( x+4 \right)\left( x-5 \right)\ge 0\Leftrightarrow \left[ \begin{align} & x\le -4 \\ & x\ge 5 \\ \end{align} \right..\)

Tập xác định: \(D=\left( -\infty ;-4 \right]\cup \left[ 5;+\infty  \right).\)

Có \(y'=\frac{2x-1}{2\sqrt{{{x}^{2}}-x-20}}\Rightarrow y'=0\Leftrightarrow 2x-1=0\Leftrightarrow x=\frac{1}{2}\)

Bảng biến thiên:

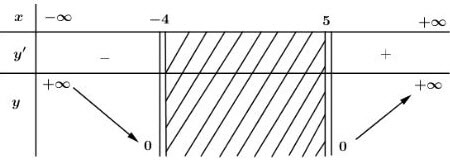
Vậy hàm số nghịch biến trên khoảng \(\left( -\infty ;-4 \right)\) và đồng biến trên khoảng \(\left( 5;+\infty  \right).\)           

* Chú ý cách tính giới hạn để điền vào bảng biến thiên:

\(\begin{align}  & \underset{x\to -\infty }{\mathop{\lim }}\,\sqrt{{{x}^{2}}-x-20}=+\infty ;\ \ \ \ \underset{x\to +\infty }{\mathop{\lim }}\,\sqrt{{{x}^{2}}-x-20}=+\infty  \\  & \underset{x\to {{4}^{-}}}{\mathop{\lim }}\,\sqrt{{{x}^{2}}-x-20}=0;\ \ \ \ \ \ \ \underset{x\to {{5}^{+}}}{\mathop{\lim }}\,\sqrt{{{x}^{2}}-x-20}=0.\  \\ \end{align}\)

d) \(y=\frac{2x}{{{x}^{2}}-9}.\)

Có \({{x}^{2}}-9\ne 0\Leftrightarrow x\ne \pm 3.\)

Tập xác định:  \(D=R\backslash \left\{ \pm 3 \right\}.\)                                                                     

Có: \(y'=\frac{2\left( {{x}^{2}}-9 \right)-2x.2x}{{{\left( {{x}^{2}}-9 \right)}^{2}}}=\frac{-2{{x}^{2}}-18}{{{\left( {{x}^{2}}-9 \right)}^{2}}}=\frac{-2\left( {{x}^{2}}+9 \right)}{{{\left( {{x}^{2}}-9 \right)}^{2}}}<0\ \forall \ x\in D.\)

Bảng biến thiên:

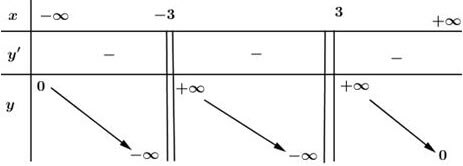
Vậy hàm số nghịch biến trên các khoảng xác định của nó là: \(\left( -\infty ;\ -3 \right);\ \left( -3;\ 3 \right)\) và \(\left( 3;\ +\infty  \right).\)

* Chú ý cách tính giới hạn để điền vào bảng biến thiên:

\(\begin{align}& \underset{x\to -\infty }{\mathop{\lim }}\,\frac{2x}{{{x}^{2}}-9}=0;\ \ \ \ \ \ \ \underset{x\to +\infty }{\mathop{\lim }}\,\frac{2x}{{{x}^{2}}-9}=0 \\ & \underset{x\to -{{3}^{+}}}{\mathop{\lim }}\,\frac{2x}{{{x}^{2}}-9}=+\infty ;\ \ \ \ \ \ \ \underset{x\to -{{3}^{-}}}{\mathop{\lim }}\,\frac{2x}{{{x}^{2}}-9}=-\infty  \\ & \underset{x\to {{3}^{+}}}{\mathop{\lim }}\,\frac{2x}{{{x}^{2}}-9}=+\infty ;\ \ \ \ \ \ \ \underset{x\to {{3}^{-}}}{\mathop{\lim }}\,\frac{2x}{{{x}^{2}}-9}=-\infty . \\ \end{align}\)

---

Trên đây là hướng dẫn giải bài 2 trang 10 SGK Giải Tích lớp 12. Mời các bạn tham khảo thêm đáp án các bài tập về giải toán 12 bài 1 hoặc hướng dẫn chi tiết các bài tập Giải tích 12 khác tại doctailieu.com.