Câu hỏi:
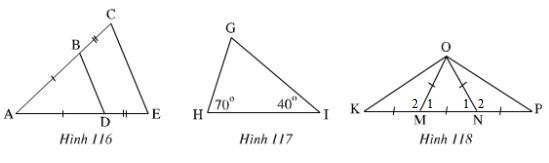
Trong cách hình 116, 117, 118 tam giác nào là tam giác cân, tam giác nào là tam giác đều? Vì sao?
Đáp án bài tập 47 sgk Hình học lớp 7 tập 1
Hình 116
Ta có: ∆ABD cân tại A vì có AB=AD.
∆ACE cân tại A vì AC=AE (do AB=AD,BC=DE nên AB+BC=AD+DE hay AC= AE).
Hình 117
Ta tính được
góc G = 180° - (góc H + I) = 180° - (70° + 40°) = 70°
Nên ∆GHI cân tại I vì (góc G = H = 70°)
Hình 118
∆OMK là tam giác cân tại M vì OM= MK
∆ONP là tam giác cân tại N vì ON=NP
∆OMN là tam giác đều vì OM = MN = ON
Do đó: góc M1 = N1 = 60° (1)
Góc M1 + M2 = 180° (hai góc kề bù) (2)
Góc N1 + N2 = 180° (hai góc kề bù) (3)
Từ (1), (2) và (3) suy ra: góc M2 = N2
Xét ∆OMK và ∆ONP có:
+) OM = ON (gt)
+) MK = NP (gt)
+) góc M2 = N2 (cmt)
⇒ ∆OMK = ∆ONP (c.g.c)
Suy ra góc MKO = NPO (Hai góc tương ứng)
Vậy ∆OKP là tam giác cân tại O.
--------------------------------------------------------------------
» Xem thêm:
giai bai tap 47 trang 127 sgk toan 7 tap 1 hinh hoc
giai bai tap 47 trang 127 sgk toan 7 tap 1 hinh hoc