Đây là tài liệu nói chi tiết và đầy đủ tam giác cân. Những nội dung ở phần tiếp theo sẽ giúp bạn
- Nắm vững định nghĩa tam giác cân là gì
- Tinh chất của tam giác cân
- Dấu hiệu nhận biết và cách chứng minh tam giác cân
Bạn đã sẵn sàng để bổ sung thêm các kiến thức hữu ích này rồi chứ
Bắt đầu nào
Tam giác cân là gì?
Tam giác cân là tam giác có hai cạnh bằng nhau, hai cạnh này được gọi là hai cạnh bên. Đỉnh của một tam giác cân là giao điểm của hai cạnh bên. Góc được tạo bởi đỉnh được gọi là góc ở đỉnh, hai góc còn lại gọi là góc ở đáy.
Trong một tam giác cân thì trực tâm, trọng tâm, tâm của đường tròn ngoại tiếp tam giác, tâm của đường tròn nội tiếp tam giác sẽ thẳng hàng với nhau. Đường thẳng đó chính là đường trung tuyến, đồng thời cũng là đường phân giác, đường trung trực và đường cao ứng với cạnh đáy.
Ví dụ
\(\Delta ABC\) cân tại A \(A \Leftrightarrow AB = AC\)
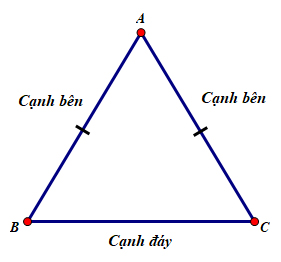
Như vậy! Bạn đã hiểu được thế nào là tam giác cân rồi chứ. Nếu muốn biết đầy đủ hơn về tính chất của tam giác cân thì xem tiếp nội dung tiếp theo nhé....
Tinh chất và dấu hiệu nhận biết tam giác cân
Tính chất
Tam giác cân có các tính chất sau
1. Trong một tam giác cân hai góc ở đáy bằng nhau.
Ví dụ: Nếu \(\Delta ABC\) cân tại \(A\) thì hai góc ở đáy \(\widehat{ABC}=\widehat{ACB}\)
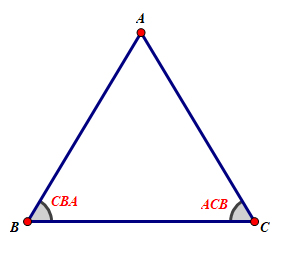
2. Một tam giác có hai góc bằng nhau thì là tam giác cân
Ví dụ: Xét tam giác \(\Delta EFG\), nếu \(\widehat{FEG}=\widehat{EGF}\) thì \(EFG\) cân tại \(F\).
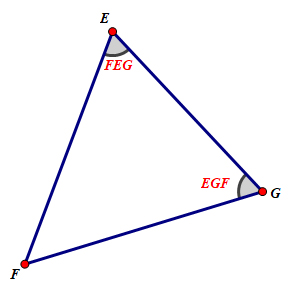
Dấu hiệu nhận biết
Dựa vào các tính chất trên thì để nhận biết tam giác cân chúng ta dựa vào số đo chiều dài của các cạnh hoặc số đo các góc.
- Nếu như một tam giác mà có hai cạnh bằng nhau thì tam giác đó là tam giác cân.
- Nếu như một tam giác mà có hai góc bằng nhau thì tam giác đó là tam giác cân.
Ở 2 phần trên, chúng ta đã nắm rất vững kiến thức thế nào là tam giác cân qua định nghĩa, tính chất và 2 dấu hiệu nhận biết. Vậy! làm thế nào để chứng minh tam giác đó là tam giác cân? Hãy xem phần nội dung tiếp theo nhé...
Cách chứng minh tam giác cân
Để chứng minh một tam giác có phải tam giác cân hay không, chúng ta dựa vào dấu hiệu nhận biết để thực hiện.
Ví dụ:
1. Chứng minh bằng 2 cạnh bằng nhau
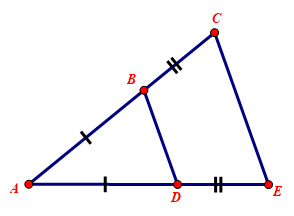
Chứng minh \(∆ABD\)cân tại \(A\)
Giải
Ta có: \(∆ABD\) cân tại \(A\) vì có \(AB=AD\)
\(∆ACE\) cân tại \(A\) vì \(AC=AE\) (do \(AB=AD,BC=DE\)nên \(AB+BC=AD+DE\) hay \(AC= AE\))
2. Chứng minh bằng 2 góc bằng nhau
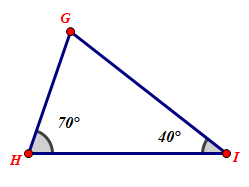
Chứng minh \(∆GHI\) cân tại \(I\)
Giải
Ta tính được
\(\widehat{G} = {180^o}- (\widehat{H}+ \widehat{I})\)\(\, = {180^0} - ({70^0} + {40^0}) = {70^0}\)
Do đó \(∆GHI\) cân tại \(I\) vì \(\widehat{G} = \widehat{H}= {70^0}\)
Kết luận chung
Như vậy! Qua bài viết này, các bạn cần ghi nhớ các nội dung sau
Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
Tính chất:
- Trong một tam giác cân hai góc ở đáy bằng nhau.
- Một tam giác có hai góc bằng nhau thì là tam giác cân
Dấu hiệu nhận biết
- Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân.
- Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân
Trên đây là các kiến thức về tam giác cân chi tiết đã được Đọc Tài Liệu biện soạn. Mong rằng, nội dung của bài viết đã giúp bạn biết được thế nào là tam giác cân, các tính chất và dấu hiệu nhận biết....
Chúc các bạn luôn vui vẻ và thành công!