Bài 8 trang 70 SGK Toán 9 tập 1

Đáp án bài 8 trang 70 SGK Toán 9 tập 1 được biên soạn bởi Đọc Tài Liệu nhằm mục đích tham khảo phương pháp làm bài. Tài liệu cũng giúp các bạn ôn tập nội dung kiến thức trong Toán 9 chương 1 phần hình học về Lý thuyết một số hệ thức về cạnh và đường cao trong tam giác vuông.

Đề bài 8 trang 70 SGK Toán 9 tập 1

Tìm \(x\) và \(y\) trong mỗi hình sau:

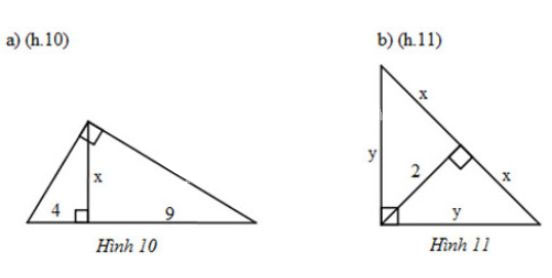
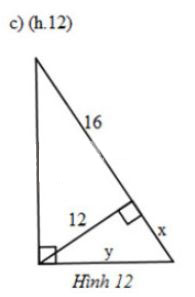
» Bài tập trước: Bài 7 trang 69 SGK Toán 9 tập 1

Giải bài 8 trang 70 SGK Toán 9 tập 1

Hướng dẫn cách làm

a) Dùng hệ thức liên quan đến đường cao và hình chiếu \(h^2=b'.c'\), biết \(b',\ c'\) tính được \(h\).

b) +) Dùng hệ thức liên quan đến đường cao và hai cạnh góc vuông \(\dfrac{1}{h^2}=\dfrac{1}{b^2}+\dfrac{1}{c^2}\) để tính \(y\).

+) Dùng định lí Pytago trong tam giác vuông để tính \(x\).

c) Dùng hệ thức liên quan đến đường cao và hình chiếu \(h^2=b'.c'\), biết \(h,\ b'\) tính được \(c'\).

+) Dùng định lí Pytago trong tam giác vuông.

Đáp án chi tiết

Dưới đây là các cách giải bài 8 trang 70 SGK Toán 9 tập 1 để các bạn tham khảo và so sánh bài làm của mình:

Đặt tên các điểm như hình vẽ:

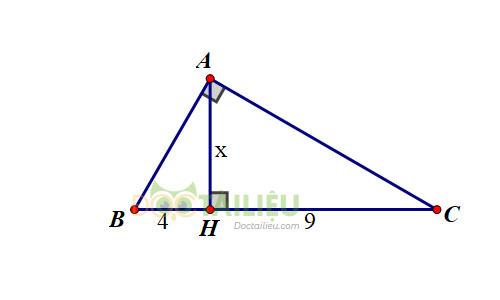
Xét \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\). Áp dụng hệ thức \(h^2=b'.c'\), ta được:

\(AH^2=BH.CH \)

\(\Leftrightarrow x^2=4.9=36\)

\(\Leftrightarrow x=\sqrt{36}=6\)

Vậy \(x=6\)

b) Đặt tên các điểm như hình vẽ

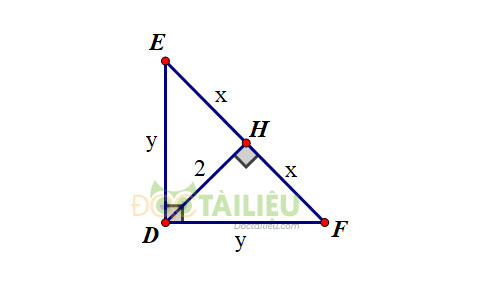
Xét \(\Delta{DEF}\) vuông tại \(D\), đường cao \(DH\). Áp dụng hệ thức \(\dfrac{1}{h^2}=\dfrac{1}{b^2}+\dfrac{1}{c^2}\), ta được:

\(\dfrac{1}{DH^2}=\dfrac{1}{DE^2}+\dfrac{1}{DF^2}\)  \(\Leftrightarrow \dfrac{1}{2^2}=\dfrac{1}{y^2}+\dfrac{1}{y^2}\)

\(\Leftrightarrow \dfrac{1}{4}=\dfrac{2}{y^2}\)

\(\Leftrightarrow y^2=4.2=8\)

\(\Leftrightarrow y=\sqrt 8=2\sqrt 2\).

Xét \(\Delta{DHF}\) vuông tại \(H\). Áp dụng định lí Pytago, ta có:

\(DF^2=DH^2+HF^2 \Leftrightarrow (2\sqrt 2)^2=2^2+x^2\)

\(\Leftrightarrow 8=4+x^2\)

\(\Leftrightarrow x^2=4\)

\(\Leftrightarrow x=\sqrt 4=2\)

Vậy \(x= 2,\ y=2\sqrt 2\).

c) Đặt tên các điểm như hình vẽ:

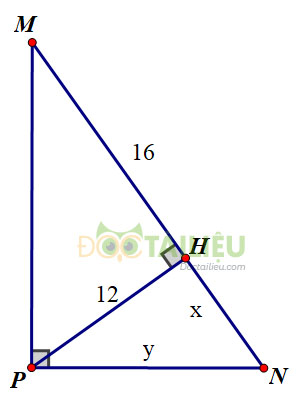
Xét \(\Delta{MNP}\) vuông tại \(P\), đường cao \(AH\). Áp dụng hệ thức \(h^2=b'.c'\), ta được:

\(PH^2=HM.HN \Leftrightarrow 12^2=16.x\)

\(\Leftrightarrow 144=16.x\)

\(\Leftrightarrow x=\dfrac{144}{16}=9\)

Xét \(\Delta{PHN}\) vuông tại \(H\). Áp dụng định lí Pytago, ta có:

\(PN^2=PH^2+HN^2 \Leftrightarrow y^2=12^2+9^2\)

\(\Leftrightarrow y^2=144+81=225\)

\(\Leftrightarrow y= \sqrt{225}=15\)

Vậy \(x=9,\ y=15\).

» Bài tiếp theo: Bài 9 trang 70 SGK Toán 9 tập 1

Nội dung trên đã giúp bạn nắm được cách làm bài 8 trang 70 SGK Toán 9 tập 1. Hy vọng những bài hướng dẫn giải Toán 9 của Đọc Tài Liệu sẽ giúp các bạn hoàn thành bài tập chính xác và học tốt môn học này.