Bài 6 trang 69 SGK Toán 9 tập 1

Lời giải bài 6 trang 69 SGK Toán 9 tập 1 được chia sẻ với mục đích tham khảo cách làm và so sánh đáp án. Cùng với đó góp phần giúp bạn ôn tập lại các kiến thức Toán 9 chương 1 phần hình học để tự tin hoàn thành tốt các bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông.

Đề bài 6 trang 69 SGK Toán 9 tập 1

Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là \(1\) và \(2\). Hãy tính các cạnh góc vuông của tam giác này.

» Bài tập trước: Bài 5 trang 69 SGK Toán 9 tập 1

Giải bài 6 trang 69 SGK Toán 9 tập 1

Hướng dẫn cách làm

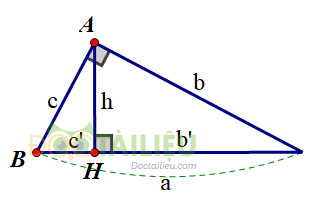
+) Tính cạnh huyền: \(a=b' +c'\).

+) Dùng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền \(b^2=b'.a;\ c^2=c'.a\), biết hình chiếu \(b',\ c'\) và cạnh huyền \(a\), tính được \(a,\ b\).

Đáp án chi tiết

Dưới đây là các cách giải bài 6 trang 69 SGK Toán 9 tập 1 để các bạn tham khảo và so sánh bài làm của mình:

Xét \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\), \(BH=1,\ CH=2\). Ta cần tính \(AB,\ AC\).

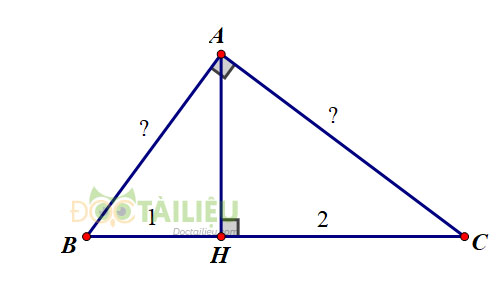
Ta có: \(BC=BH+HC=1+2=3\)

Áp dụng hệ thức lượng trong \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\), ta có:

* \(AB^2=BH.BC \Leftrightarrow AB^2=1.3=3\)

\(\Leftrightarrow AB = \sqrt 3\)

* \( AC^2=CH.BC \Leftrightarrow AC^2=2.3=6\)

\(\Leftrightarrow AC=\sqrt 6\)

Vậy độ dài hai cạnh góc vuông cần tìm là \(\sqrt 3\) và \(\sqrt 6\).

» Bài tiếp theo: Bài 7 trang 69 SGK Toán 9 tập 1

Nội dung trên đã giúp bạn nắm được cách làm bài 6 trang 69 SGK Toán 9 tập 1. Hy vọng những bài hướng dẫn giải Toán 9 của Đọc Tài Liệu sẽ giúp các bạn hoàn thành bài tập chính xác và học tốt môn học này.