Bài 7 trang 69 SGK Toán 9 tập 1

Những nội dung dưới đây không chỉ giúp bạn biết được cách làm, tham khảo đáp án bài 7 trang 69 SGK Toán 9 tập 1 mà còn hỗ trợ bạn ôn tập để nắm vững các kiến thức chương 1 phần hình học Toán 9 về Lý thuyết một số hệ thức về cạnh và đường cao trong tam giác vuông đã được học trên lớp.

Đề bài 7 trang 69 SGK Toán 9 tập 1

Người ta đưa ra hai cách vẽ đoạn trung bình nhân $x$ của hai đoạn thẳng $a,\ b$ (tức là ${x^2} = ab$ ) như trong hai hình sau:

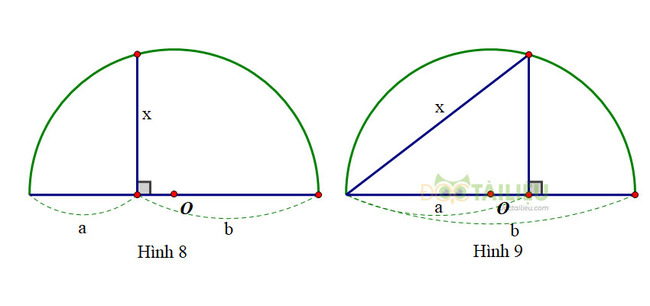
Dựa vào các hệ thức (1) và (2), hãy chứng minh các cách vẽ trên là đúng.

Gợi ý: Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.

» Bài tập trước: Bài 6 trang 69 SGK Toán 9 tập 1

Giải bài 7 trang 69 SGK Toán 9 tập 1

Hướng dẫn cách làm

+) Đặt tên các điểm và nối các điểm lại để xuất hiện tam giác.

+) Dùng dấu hiệu: "tam giác có đường trung tuyến ứng với cạnh huyền bằng nửa cạnh đó là tam giác vuông" để chứng minh tam giác vuông.

+ Dùng các hệ thức sau để chứng minh $x$ là trung bình nhân của $a,\ b$:

$b^2=a.b',\ c^2=a.c'$      $(1)$

$h^2=b'.c'$                       $(2)$

+) Nêu các bước để vẽ được đoạn trung bình nhân.

Đáp án chi tiết

Dưới đây là các cách giải bài 7 trang 69 SGK Toán 9 tập 1 để các bạn tham khảo và so sánh bài làm của mình:

Cách 1: Đặt tên các đoạn thẳng như hình bên.

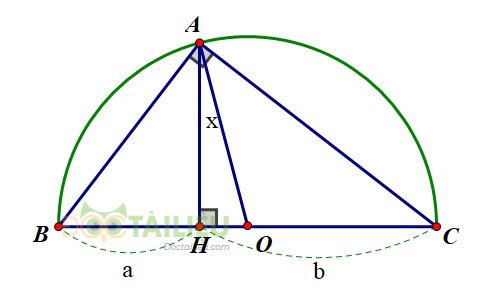
Xét $\Delta{ABC}$ có:

$OA = OB = OC = \dfrac{BC}{2}$ (cùng bằng bán kính đường tròn (O))

Mà $AO$ là trung tuyến ứng với cạnh $BC$ của $\Delta{ABC}$.

Suy ra $\Delta{ABC}$ vuông tại $A$ ( tam giác có đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền thì là tam giác vuông)

Xét $\Delta{ABC}$ vuông tại $A$, đường cao $AH$. Áp dụng hệ thức $h^2=b'.c'$, ta được:

$AH^2=BH.CH \Leftrightarrow x^2=a.b$

$\Leftrightarrow x=\sqrt {ab}$

Vậy $x$ là trung bình nhân của $a$ và $b$.

Cách vẽ: Bước $1$: Đặt $BH=a,\ CH=b$. Xác định trung điểm $O$ của đoạn $AB$.

Bước $2$: Vẽ nửa đường tròn tâm $O$ bán kính $OB$.

Bước $3$: Kẻ thẳng đi qua $H$ và vuông góc với $BC$. Đường thẳng này cắt nửa đường tròn tại $A$.

Bước $4$: Nối $A$ và $H$ ta được $AH=x$ là đoạn trung bình nhân của hai đoạn thẳng $a,\ b$.

Cách 2: Vẽ và đặt tên như hình bên dưới

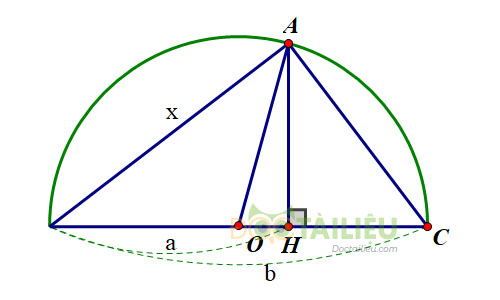
Xét $\Delta{ABC}$ có:

$OA = OB = OC = \dfrac{BC}{2}$ (cùng bằng bán kính đường tròn (O))

Mà $AO$ là trung tuyến ứng với cạnh $BC$ của $\Delta{ABC}$.

Suy ra $\Delta{ABC}$ vuông tại $A$ (tam giác có đường trung tuyến ứng với cạnh huyền bẳng nửa cạnh đó thì là tam giác vuông)

Xét $\Delta{ABC}$ vuông tại $A$, đường cao $AH$.  Áp dụng hệ thức $b^2=b'.a$, ta có:

$AB^2 = BC.BH \Leftrightarrow x^2=a.b$

$\Leftrightarrow x=\sqrt{ab}$

Vậy $x$ là trung bình nhân của $a$ và $b$.

Cách vẽ: Bước $1$: Đặt $BH=a,\ CH=b$. Xác định trung điểm $O$ của đoạn $BC$.

Bước $2$: Vẽ nửa đường tròn tâm $O$ bán kính $OB$.

Bước $3$: Kẻ đường thẳng đi qua điểm $H$. Đường thẳng này cắt nửa đường tròn tại $A$.

Bước $4$: Nối $B$ và $A$ ta được $AB=x$ là đoạn trung bình nhân của hai đoạn thẳng $a,\ b$.

» Bài tiếp theo: Bài 8 trang 70 SGK Toán 9 tập 1

Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 7 trang 69 SGK Toán 9 tập 1. Mong rằng những bài hướng dẫn giải Toán 9 của Đọc Tài Liệu sẽ là người đồng hành giúp các bạn học tốt môn học này.