Bài 43 trang 121 SGK Toán 8 tập 2

Lời giải bài 43 trang 121 sgk Toán 8 tập 2 được chia sẻ với mục đích tham khảo cách làm và so sánh đáp án. Cùng với đó góp phần giúp bạn ôn tập lại các kiến thức Toán 8 chương 4 phần hình học để tự tin hoàn thành tốt các bài tập diện tích xung quanh của hình chóp đều khác.

Đề bài 43 trang 121 SGK Toán 8 tập 2

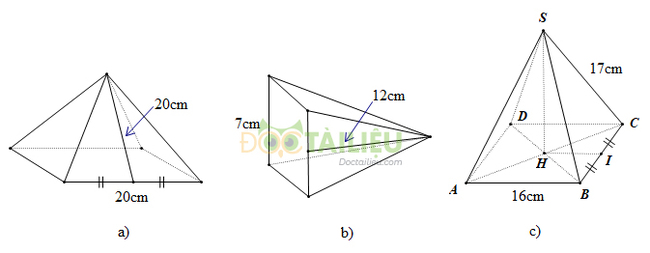
Tính diện tích xung quanh, diện tích toàn phần của các hình chóp tứ giác đều sau đây.(h.126)

» Bài tập trước: Bài 42 trang 121 SGK Toán 8 tập 2

Giải bài 43 trang 121 sgk Toán 8 tập 2

Hướng dẫn cách làm

- Tính diện tích xung quanh: \(S_{xq}= p.h \), trong đó \(p\) là nửa chu vi đáy, \(d\) là trung đoạn của hình chóp đều.

- Tính diện tích đáy theo công thức diện tích hình vuông: \(S_{hv}\) = cạnh \(\times \) cạnh.

- Tính diện tích toàn phần: \(S_{tp}= S_{xq} + S_{đ}\)

Bài giải chi tiết

Dưới đây là các cách giải bài 43 trang 121 SGK Toán 8 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

+) Hình a :

Diện tích xung quanh của lăng trụ là:

\(S_{xq}= p.d = \dfrac{1}{2}.20.4.20 = 800(cm^2) \)

Diện tích đáy là:

\( S_{đ} = 20^2 = 400(cm^2) \)

Diện tích toàn phần của lăng trụ là:

\( S_{tq}= S_{xq} + S_{đ} = 800 + 400 = 1200\) \((cm^2) \)

+) Hình b:

Diện tích xung quanh của lăng trụ là:

\(S_{xq}= p.d = \dfrac{1}{2}.7.4.12 = 168 (cm^2) \)

Diện tích đáy là:

\( S_{đ} = 7^2 = 49(cm^2) \)

Diện tích toàn phần của lăng trụ là:

\( S_{tq}= S_{xq} + S_{đ} = 168 + 49 = 217\)\(\,(cm^2) \)

+) Hình c:

Chiều cao của các mặt bên của hình chóp là:

\(d = \sqrt{17^{2}- 8^{2}}= \sqrt{225} = 15(cm) \)

Diện tích xung quanh của lăng trụ là:

\(S_{xq}= p.d = \dfrac{1}{2}.16.4.15 = 480(cm^2) \)

Diện tích đáy là:

\( S_{đ} = 16^2 = 256(cm^2) \)

Diện tích toàn phần của lăng trụ là:

\( S_{tq}= S_{xq} + S_{đ} = 480 + 256 = 736\) \((cm^2) \)

» Bài tập tiếp theo: Bài 44 trang 123 SGK Toán 8 tập 2

Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 43 trang 121 sgk toán 8 tập 2. Mong rằng những bài hướng dẫn giải toán 8 của Đọc Tài Liệu sẽ là người đồng hành giúp các bạn học tốt môn học này.