Bài 42 trang 121 SGK Toán 8 tập 2

Lời giải bài 42 trang 121 sgk Toán 8 tập 2 được chia sẻ với mục đích tham khảo cách làm và so sánh đáp án. Cùng với đó góp phần giúp bạn ôn tập lại các kiến thức Toán 8 chương 4 phần hình học để tự tin hoàn thành tốt các bài tập diện tích xung quanh của hình chóp đều khác.

Đề bài 42 trang 121 SGK Toán 8 tập 2

Tính độ dài đường cao của hình chóp tứ giác đều với các kích thước cho ở hình 125.

» Bài tập trước: Bài 41 trang 121 SGK Toán 8 tập 2

Giải bài 42 trang 121 sgk Toán 8 tập 2

Hướng dẫn cách làm

Áp dụng định lý Pytago trong tam giác vuông.

Bài giải chi tiết

Dưới đây là các cách giải bài 42 trang 121 SGK Toán 8 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

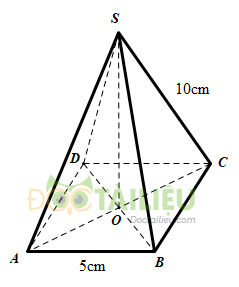
Gọi \(O\) là giao điểm hai đường chéo của hình vuông đáy.

Tam giác \(ABC\) vuông tại \(B\) nên ta có :

\( AC^2 = AB^2 + BC^2 \)\(\,= 5^2 + 5^2 = 50 \)

Tam giác \(SOC\) vuông tại \(O\) nên ta có:

\( SO^2 + OC^2 = SC^2\)

\( \Rightarrow SO^2 = SC^2 - OC^2 \)\(\,=  SC^2 - {\left( {\dfrac{{AC}}{2}} \right)^2}\)

\( SO =  \sqrt{SC^{2}- {\left( {\dfrac{{AC}}{2}} \right)^2}}\)\(\,= \sqrt{10^{2}- \dfrac{50}{4}}\) \(\approx 9,35\, (cm)\)

» Bài tập tiếp theo: Bài 43 trang 121 SGK Toán 8 tập 2

Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 42 trang 121 sgk toán 8 tập 2. Mong rằng những bài hướng dẫn giải toán 8 của Đọc Tài Liệu sẽ là người đồng hành giúp các bạn học tốt môn học này.