Bài 40 trang 121 SGK Toán 8 tập 2

Lời giải bài 40 trang 121 sgk Toán 8 tập 2 được chia sẻ với mục đích tham khảo cách làm và so sánh đáp án. Cùng với đó góp phần giúp bạn ôn tập lại các kiến thức Toán 8 chương 4 phần hình học để tự tin hoàn thành tốt các bài tập diện tích xung quanh của hình chóp đều khác.

Đề bài 40 trang 121 SGK Toán 8 tập 2

Một hình chóp tứ giác đều có độ dài cạnh bên bằng \(25cm\), đáy là hình vuông \(ABCD\) cạnh \(30cm\).

Tính diện tích toàn phần của hình chóp.

» Bài tập trước: Bài 39 trang 121 SGK Toán 8 tập 2

Giải bài 40 trang 121 sgk Toán 8 tập 2

Hướng dẫn cách làm

- Tính diện tích xung quanh: \(S_{xq}= p.d \), trong đó \(p\) là nửa chu vi đáy, \(d\) là trung đoạn của hình chóp đều.

- Tính diện tích đáy theo công thức diện tích hình vuông: \(S_{hv}\) = cạnh \(\times \) cạnh.

- Tính diện tích toàn phần: \(S_{tp}= S_{xq} + S_{đ}\)

Bài giải chi tiết

Dưới đây là các cách giải bài 40 trang 121 SGK Toán 8 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

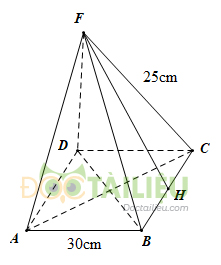
Gọi \(H\) là trung điểm của \(BC\).

Khi đó ta có: \(BH = HC = \dfrac{1}{2}BC =\dfrac{1}{2}. 30=15 \,cm  \)

Vì tam giác \(SBC\) cân tại \(S\) nên \( SH\perp BC \).

Ta có:  \(d = SH = \sqrt{SB^2- BH^2}\) \( = \sqrt{25^2 -15^2} = \sqrt{400}=20(cm)\)

Diện tích xung quanh của hình chóp:

\(S_{xq} = p.d =\dfrac{1}{2} .30.4.20 = 1200 (cm^2) \)

Diện tích đáy là:

\( S_{đ} = 30.30 = 900 (cm^2)\)

Diện tích toàn phần của hình chóp là:

\( S_{tp} =S_{xq}+ S_{đ} = 1200 + 900 \) \(= 2100 (cm^2) \)

» Bài tập tiếp theo: Bài 41 trang 121 SGK Toán 8 tập 2

Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 40 trang 121 sgk toán 8 tập 2. Mong rằng những bài hướng dẫn giải toán 8 của Đọc Tài Liệu sẽ là người đồng hành giúp các bạn học tốt môn học này.