Mời bạn đọc tham khảo đề thi vào lớp 10 môn Toán chính thức từ Sở Giáo dục và Đào tạo tỉnh Thái Bình năm học 2024 - 2025 kèm đáp án chi tiết được cập nhật bên dưới.
Đề thi tuyển sinh lớp 10 môn Toán tỉnh Thái Bình năm 2024
Đề thi và đáp án môn Toán kỳ thi vào lớp 10 năm 2024 tại tỉnh Thái Bình sẽ được Đọc Tài Liệu cập nhật ngay khi môn thi kết thúc.






Xem thêm thông tin
- Tra cứu điểm thi tuyển sinh lớp 10 năm 2024 Thái Bình
- Điểm chuẩn lớp 10 năm 2024 tỉnh Thái Bình
- Đáp án đề thi tuyển sinh vào lớp 10 môn Văn tỉnh Thái Bình
- Đáp án đề thi tuyển sinh vào lớp 10 môn Anh tỉnh Thái Bình
Tham khảo đề thi và đáp án môn Toán tỉnh Thái Bình các năm trước bên dưới:
Đề thi tuyển sinh lớp 10 môn Toán tỉnh Thái Bình năm 2023
ĐỀ THI

ĐÁP ÁN THAM KHẢO
(Đáp án chỉ mang tính chất tham khảo, không phải đáp án chính thức.)
Câu 1.
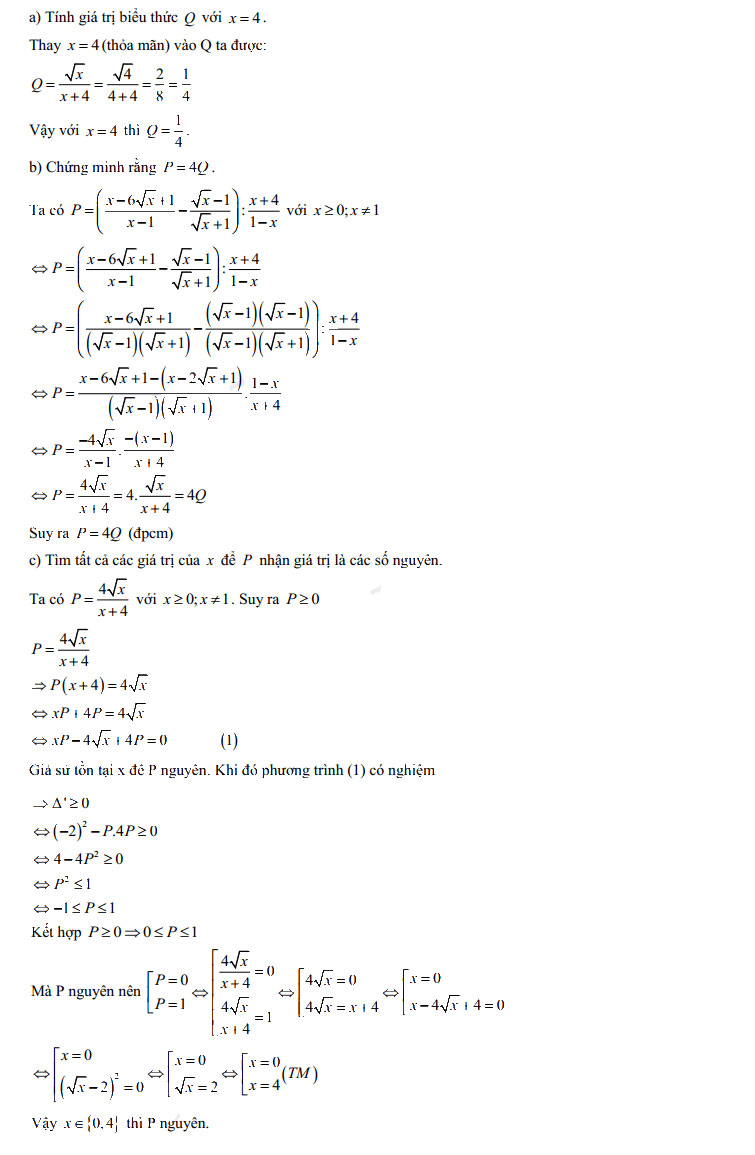
Câu 2.

Câu 3.

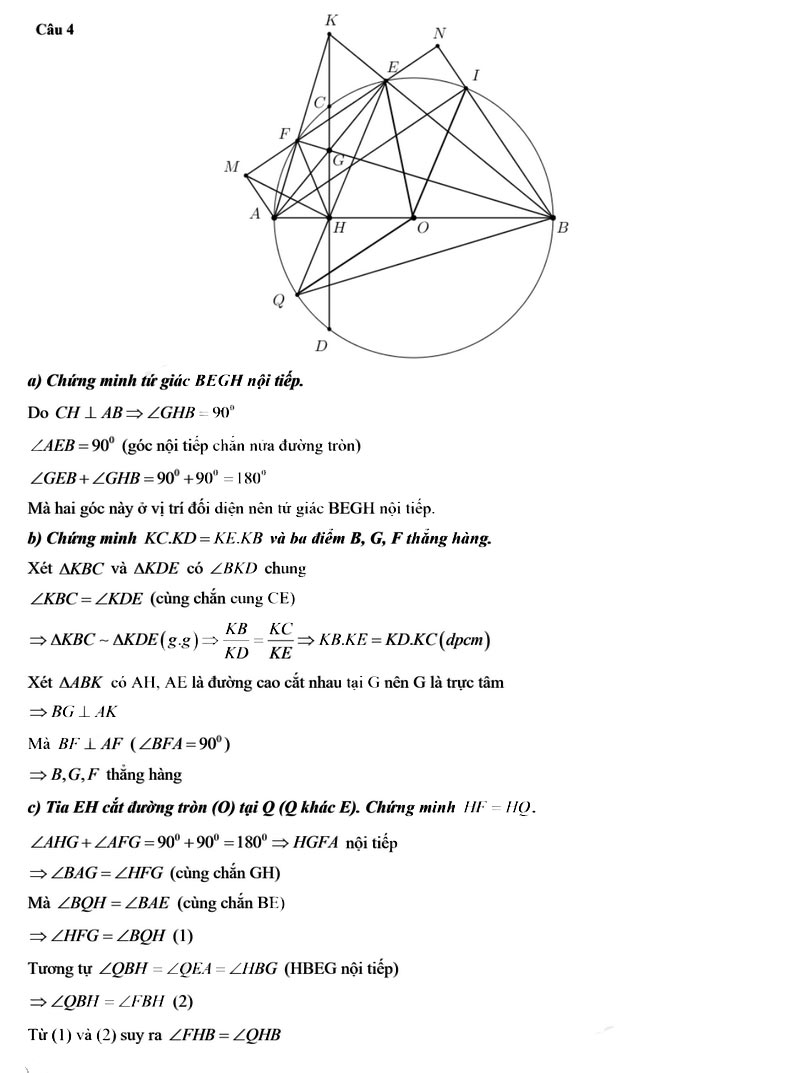
Câu 4.
1) Cho tam giác ABC nhọn, nội tiếp đường tròn (O;R). Kẻ AH vuông góc với BC tại H, HK vuông góc với AB tại K và HI vuông góc với AC tại I .
a) Chứng minh tứ giác AKHI nội tiếp.
b) Gọi E là giao điểm của AH với KI. Chứng minh rằng EAEH = EK.EI .
c) Chứng minh KI vuông góc với AO.
d) Giả sử điểm A và đường tròn (O;R) cố định, còn đây cung BC thay đổi sao cho AB.AC = 3R² . Xác định vị trí của dây cung BC sao cho tam giác ABC có diện tích lớn nhất.
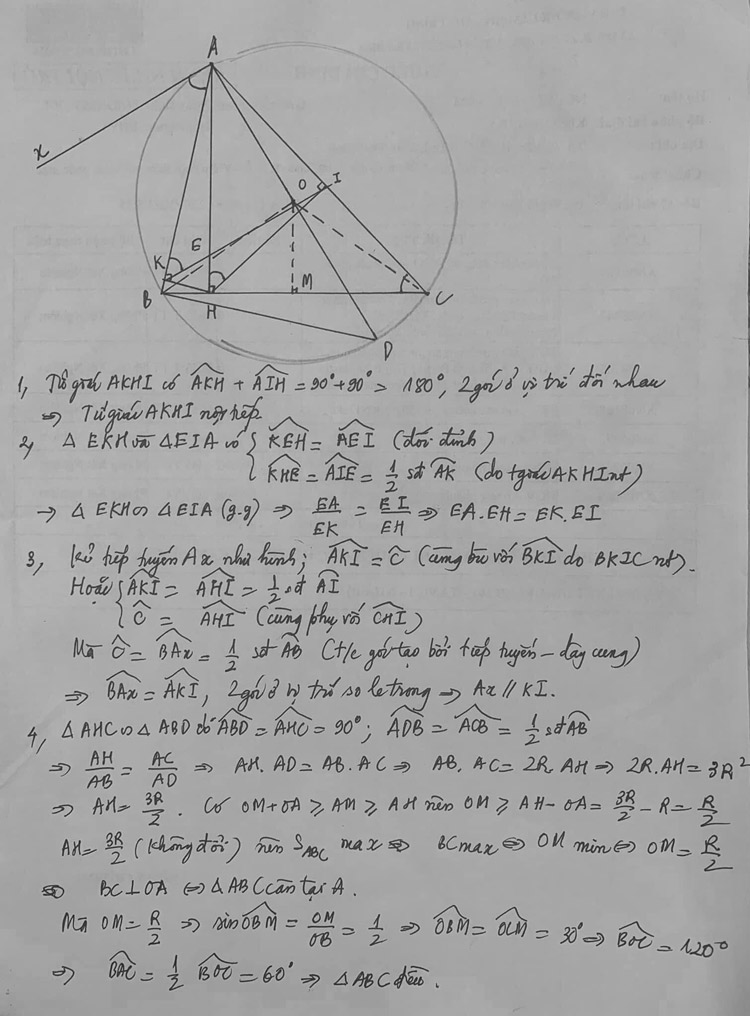
2) Một hình nón có diện tích đáy bằng 16π(cm²) và có chiều cao gấp ba lần bán kính đáy. Tính thể tích của hình nón đó.
Vì diện tích đáy bằng 16π nên ta có πR²=16π
=> R = 4 (cm)
Lại có chiều cao gấp ba lần bán kính đáy
=> h = 3. R = 12 (cm)
Vậy thể tích khối nón là:
\(V = \dfrac{1}{3}πR²h = \dfrac{1}{3}π 4^2.12= 64π\) (cm³).
Kết luận:....
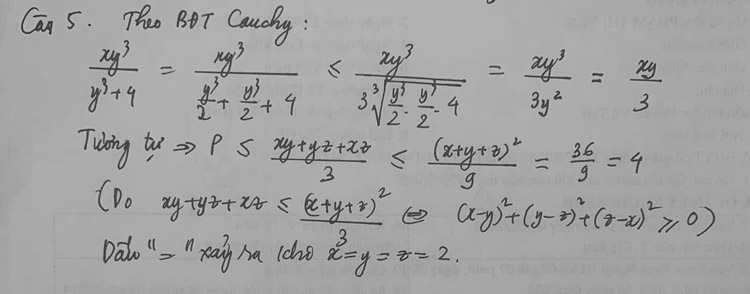
Đề thi tuyển sinh lớp 10 môn Toán tỉnh Thái Bình năm 2022
ĐỀ THI
Câu 4. (3,5 điểm)
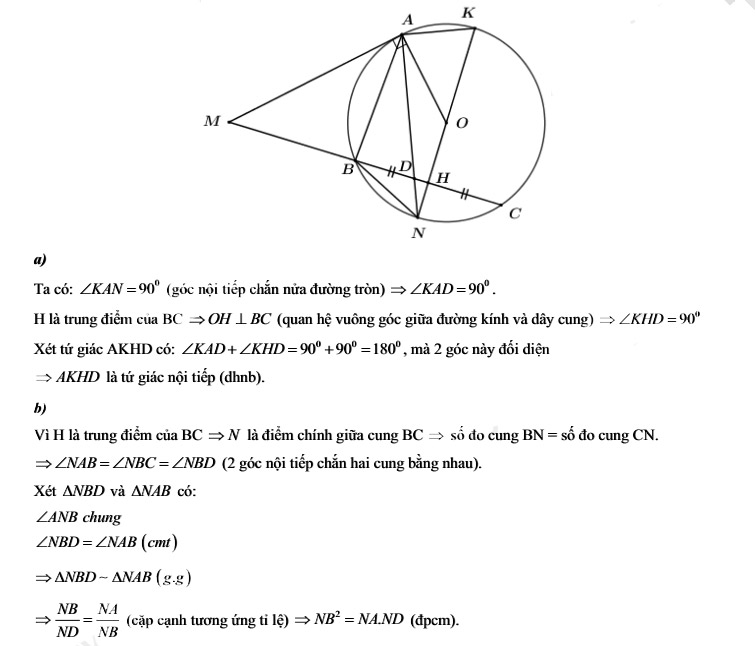
1) Từ điểm M nằm ngoài đường tròn (O;R) kẻ tiếp tuyến MA (A là tiếp điểm) và cát tuyến MBC không đi qua tâm O (điểm A nằm giữa hai điểm M và C). Gọi H là trung điểm BC. Đường thẳng OH cắt đường tròn (O;R) tại hai điểm. N,K (trong đó điểm K thuộc cung BAC). Gọi D là giao điểm của AN và BC.
a) Chứng minh tứ giác AKHD là tứ giác nội tiếp.
b) Chứng minh: ∠NAB = ∠NBD và NB² = NA.ND.
c) Chứng minh rằng khi đường tròn (O;R) và điểm M cố định đồng thời các tuyến MBC thay đổi thì điểm D nằm trên một đường tròn cố định.

Đáp án đề thi tuyển sinh lớp 10 môn Toán năm 2022 Thái Bình
Câu 1

Câu 2

Câu 3

Câu 4.
1.
2.
Ta có chu vi đáy C = 2πR = 20π ⇒ R = 10 (cm)
Thể tích hình trụ là V = πR²h = π.10².7 = 700π (cm³).
Câu 5.
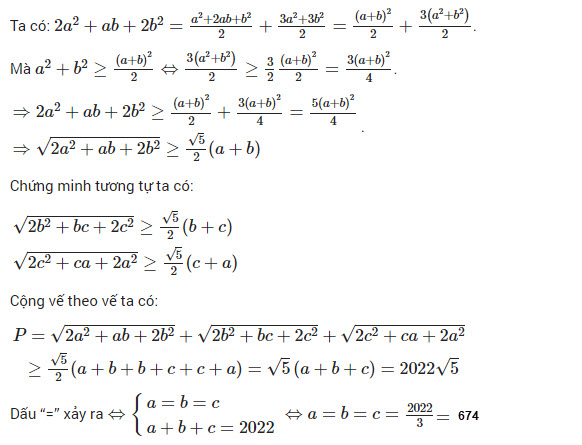
Đề thi vào lớp 10 môn Toán tỉnh Thái Bình năm 2021
Kỳ thi tuyển sinh vào lớp 10 của tỉnh Thái Bình sẽ diễn ra trong 2 ngày 19/06/2021-20/06/2021 sắp tới. Đề thi chính thức vào lớp 10 môn Toán năm 2021 tỉnh Thái Bình sẽ được cập nhật ngay sau khi kỳ thi diễn ra.

Đáp án đề thi vào lớp 10 môn Toán 2021 tỉnh Thái Bình
Câu 1.
a)
\(\begin{aligned} &\text { Điều kiện: } x \geq 0, x \neq 4 . \\ &P=\dfrac{1}{\sqrt{x}-2}-\dfrac{2}{\sqrt{x}+1}+\dfrac{2 \sqrt{x}-7}{x-\sqrt{x}-2} \\ &=\dfrac{1}{\sqrt{x}-2}-\dfrac{2}{\sqrt{x}+1}+\dfrac{2 \sqrt{x}-7}{(\sqrt{x}+1)(\sqrt{x}-2)} \\ &=\dfrac{\sqrt{x}+1-2(\sqrt{x}-2)+2 \sqrt{x}-7}{(\sqrt{x}+1)(\sqrt{x}-2)} \\ &=\dfrac{\sqrt{x}+1-2 \sqrt{x}+4+2 \sqrt{x}-7}{(\sqrt{x}+1)(\sqrt{x}-2)} \\ &=\dfrac{\sqrt{x}-2}{(\sqrt{x}+1)(\sqrt{x}-2)} \\ &=\dfrac{1}{\sqrt{x}+1} . \\ &\text { Vậy vói } x \geq 0, x \neq 4 \text { thì } P=\dfrac{1}{\sqrt{x}+1} . \end{aligned}\)
b)
Điều kiện: \(x \geq 0, x \neq 4.\)
Ta có: \(x=3-2 \sqrt{x}=(\sqrt{2}-1)^{2}\) thỏa mãn điều kiện.
\(\Rightarrow \sqrt{x}=\sqrt{3-2 \sqrt{2}}=\sqrt{(\sqrt{2}-1)^{2}}=|\sqrt{2}-1|=\sqrt{2}-1\,\,( \,do \,\,\sqrt{2}-1>0)\)
Thay \(\sqrt{x}=\sqrt{2}-1\) vào biểu thức P ta được:
\( P=\dfrac{1}{\sqrt{x}+1}=\dfrac{1}{\sqrt{2}-1+1}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}.\)
Vậy với \(x=3-2 \sqrt{2}\) thì \(P=\dfrac{\sqrt{2}}{2}.\)
c)
Điều kiện: \(x \geq 0, x \neq 4.\)
Ta có: \(P=\dfrac{1}{\sqrt{x}+1}.\)
Với \(\forall x \geq 0, x \neq 4\) ta có: \(\sqrt{x} \geq 0 \Rightarrow \sqrt{x}+1 \geq 1\)
\(\Rightarrow \frac{1}{\sqrt{x}+1} \leq 1 \Rightarrow P \leq 1\)
Dấu "=" xảy ra \(\Leftrightarrow \sqrt{x}+1=1 \Leftrightarrow \sqrt{x}=0 \Leftrightarrow x=0\,({tm})\)
Vậy với x = 0 thì giá trị lớn nhất của P là 1 .
Câu 2:
a)
Phương trình \(x^{2}+3 x-1=0\) có: \(\Delta=(-3)^{2}-4 \cdot(-1)=13>0\)
=> Phương trình có hai nghiệm phân biệt \(x_{1}=\frac{-3+\sqrt{13}}{2} \,\,và\, \,x_{2}=\frac{-3-\sqrt{13}}{2}.\)
Vậy phương trình có tập nghiệm: \(S=\left\{\frac{-3-\sqrt{13}}{2} ; \frac{-3+\sqrt{13}}{2}\right\}.\)
b)
Nửa chu vi của mảnh vườn đã cho là: 60: 2=30 (m).
Gọi chiều dài và chiều rộng của mảnh vườn lần lượt là x, y(m), (\(0<><>).
\(\Rightarrow x+y=30\)
Nểu giảm chiều dài đi 1m và tăng chiều rộng lên 1m thì mảnh vườn trở thành hình vuông nên ta có phương trình: \(x-1=y+1 \Leftrightarrow x-y=2(2)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{\begin{array}{l}x+y=30 \\ x-y=2\end{array} \Leftrightarrow\left\{\begin{array}{l}2 x=32 \\ y=x-2\end{array} \Leftrightarrow\left\{\begin{array}{l}x=16(t m) \\ y=16-2\end{array} \Leftrightarrow\left\{\begin{array}{l}x=16 \\ y=14(t m)\end{array}\right.\right.\right.\right.\)
Vậy chiều dài mảnh vườn là 16m và chiều rộng mảnh vườn là 14m.
Câu 3.
a)
Gọi \(A\left(2 ; y_{A}\right)\) là điểm mà đường thẳng (d) và parabol (P) đều đi qua.
Khi đó ta có:
\(A\left(2 ; y_{A}\right) \in(P) \Rightarrow y_{A}=2^{2}=4 \Rightarrow A(2 ; 4).\)
Lại có: \(A(2 ; 4) \in(d) \Rightarrow 4=m .2+1 \Leftrightarrow m=\frac{3}{2}\)
Vậy \( m=\dfrac{3}{2}\) thỏa mãn bài toán.
b)
Phương trình hoành độ giao điềm của (d) và (P) là: \(x^{2}=m x+1 \Leftrightarrow x^{2}-m x-1=0\)(*)
Phương trình (*) có: \(\Delta=m^{2}+4>0 \forall m\)
⇒(*) luôn có hai nghiệm phân biệt với mọi m.
⇒(d) luôn cắt (P) tại hai điểm phân biệt với mọi m.
Gọi \(x_{1}, x_{2}\) là các hoành độ giao điểm của (d) và (P) ⇒ \(x_{1}, x_{2}\) là các nghiệm của phương trình (*).
\(⇒ x_{1}^{2}=m x_{1}+1\)
Áp dụng hệ thức Vi-et ta có:
\(\left\{\begin{array}{l}x_{1}+x_{2}=m \\ x_{1} x_{2}=-1\end{array}\right.\).
Theo đề bài ta có: \(x_{2}\left(x_{1}^{2}-1\right)=3\)
\(\Leftrightarrow x_{2}\left(m x_{1}+1-1\right)=3\)
\(\Leftrightarrow m x_{1} x_{2}=3\)
\(\Leftrightarrow-m=3\)
\(\Leftrightarrow m=-3\)
Vậy m = -3 thỏa mãn bài toán.
Câu 4
a)
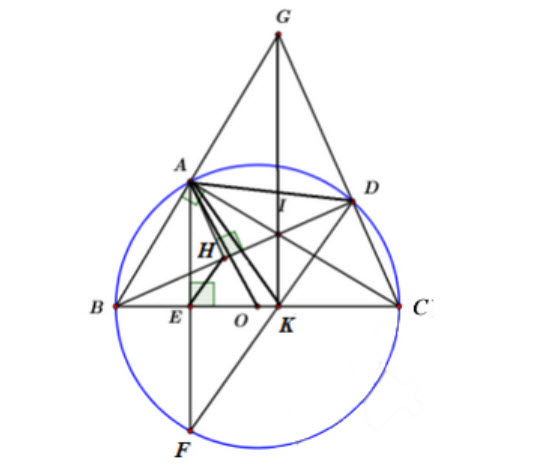
Ta có: ∠BAC, ∠BDC là góc nội tiếp chắn nửa đường tròn (0)
∠BAC =∠BDC = 90°.
=> ∠GAI = ∠GDI = 90°
Xét tứ giác AIDG ta có: ∠GAI +∠GDI = 90° +90° =180°
=> AIDG là tứ giác nội tiếp.
b) Xét tứ giác ABEH ta có: ∠AEB = ∠AHB = 90° (gt)
=> ABEH là tứ giác nội tiếp. (tứ giác có hai đỉnh kề nhau cùng nhìn cạnh đối diện dưới các góc bằng nhau)
∠BHE =∠BAE (hai góc nội tiếp cùng chắn cung BE)
Mà ∠BAE =∠BCA (hai góc cùng phụ ∠ABC)
∠BHE = ∠BCA= ∠BCI
Xét △BHE và △BCI có:
∠IBC chung
∠BHE = ∠BCI (cmt)
=> △BHE ∽ △BCI (g-g)
\(\Rightarrow \dfrac{B E}{B I}=\dfrac{B H}{B C} \Rightarrow B E \cdot B C=B H \cdot B I(d p c m) .\)
c)
Ta có: B C ⊥ A F => cung AB = cung FB (đường kinh vuông góc với một dây thì đi qua điểm ở chinh giữa của cung căng dây đó).
⇒ ∠BDF=∠BCA (hai góc nội tiếp chẳn 2 cung bằng nhau).
Hay ∠I D K=∠ICK
⇒ CDJK là tức giác nội tiếp. (tứ giác có 2 đỉnh kề nhau củng nhìn 1 cạnh dưới các góc bằng nhau)
⇒ ∠IKC+∠IDC = 180⁰.
Mà ∠IDC=∠BDC=90⁰(cmt)
⇒ ∠IKC=90⁰ => IK ⊥ BC
\(\begin{aligned} &\text { Xét } \triangle G B C \text { có }\left\{\begin{array}{l} A C \perp B G \\ B D \perp C G \\ A C \cap B D=\{I\} \end{array}\right.\\ &\Rightarrow I \text { là trực tâm } \Delta G B C \Rightarrow G I \perp B C \text { (2) }\\ &\text { Từ (1) và }(2) \Rightarrow G, I, K \text { thẳng hàng. (đpcm) } \end{aligned}\)

Câu 5

-/-
Cùng ôn tập chuẩn bị thật tốt cho kỳ thi sắp tới với đề thi tuyển sinh lớp 10 các năm trước nhé:
Đề thi tuyển sinh lớp 10 môn Toán tỉnh Thái Bình năm 2020
Câu 1. (2,0 điểm)
Cho \(A=\frac{\sqrt{x}+1}{\sqrt{x}-1}\) và \(B=\left(\frac{\sqrt{x}+1}{\sqrt{x}-1}-\frac{\sqrt{x}-1}{\sqrt{x}+1}\right): \frac{\sqrt{x}}{\sqrt{x-1}}\) (với \(x>0 ; x \neq 1\))
a) Tính giá trị biểu thức A khi x=9
b) Rút gọn biểu thức B
c) Tìm x để giá trị của A và B trái dấu
Xem chi tiết đề thi và đáp án tại link: Đề thi vào lớp 10 môn Toán 2020 Thái Bình
Đề thi tuyển sinh lớp 10 môn Toán tỉnh Thái Bình năm 2019
Câu 1. (2,0 điểm)
Cho \(A=\frac{x+\sqrt{x}+1}{\sqrt{x}+1}\) và \(B=\frac{1}{\sqrt{x}-1}-\frac{x+2}{x \sqrt{x}-1}-\frac{\sqrt{x}+1}{x+\sqrt{x}+1}\) (với \(x \geq 0, x \neq 1\) )
a) Tính giá trị biểu thức A khi x=2
b) Rút gọn biểu thức B
c) Tìm x sao cho biểu thức C= -A.B nhận giá trị là số nguyên.
Xem chi tiết đề thi và đáp án tại link: Đề thi vào lớp 10 môn Toán tỉnh Thái Bình năm 2019 có đáp án
Đề thi tuyển sinh lớp 10 môn Toán tỉnh Thái Bình năm 2018
Câu 1. (2,0 điểm)
a) Tìm x để biểu thức sau có nghĩa \(P=\sqrt{5 x+3}+2018 \cdot \sqrt[3]{x}\)
b) Cho hàm số \(y=\frac{1}{2} x^{2}\) . Điểm D có hoành độ x= -2 thuộc đồ thị hàm số. Tìm tọa độ điểm D
c) Tìm giá trị của a và b để đường thẳng d: y=ax+b-1 đi qua 2 điểm A(1;1) và B(2;3)
Xem chi tiết đề thi và đáp án tại link: Đề thi Toán vào lớp 10 tỉnh Thái Bình 2018
Trên đây là toàn bộ nội dung của đề thi tuyển sinh lớp 10 môn Toán 2024 và các năm trước mà Đọc Tài Liệu chia sẻ nhằm giúp các em nắm được các thông tin về kỳ thi này.
Mong rằng những tài liệu của chúng tôi sẽ là người đồng hành giúp các bạn hoàn thành tốt bài thi của mình.
