Đề thi tuyển sinh vào lớp 10 môn Toán năm 2024-2025 chính thức của Sở Giáo dục và Đào Tạo tỉnh Hà Nam được cập nhật nhanh nhất. Cùng Đọc tài liệu tham khảo ngay.
Đề thi vào 10 môn Toán tỉnh Hà Nam 2024
Đề thi và đáp án môn Toán kỳ thi vào lớp 10 năm 2024 tại tỉnh Hà Nam sẽ được Đọc Tài Liệu cập nhật ngay khi môn thi kết thúc.
ĐÁP ÁN THAM KHẢO



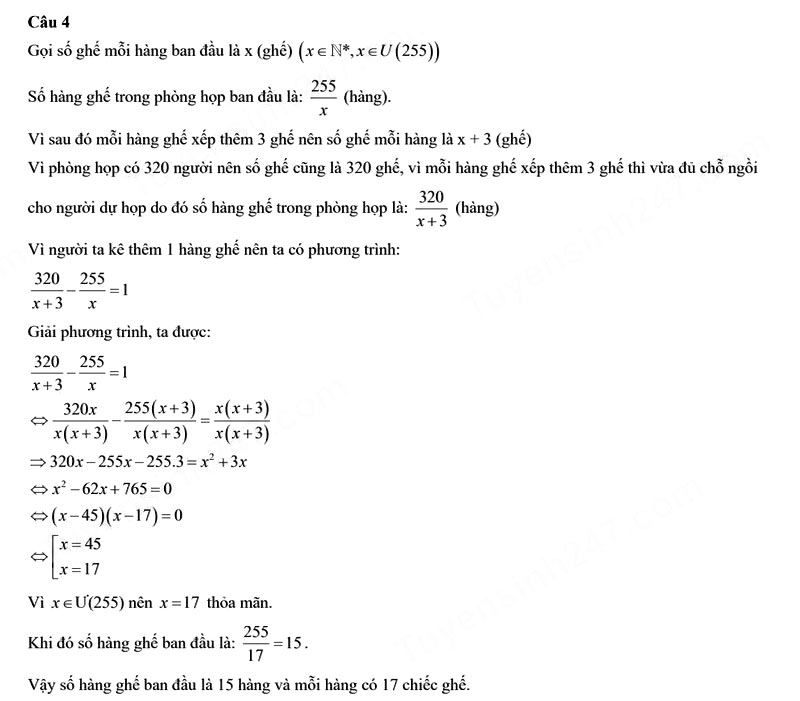

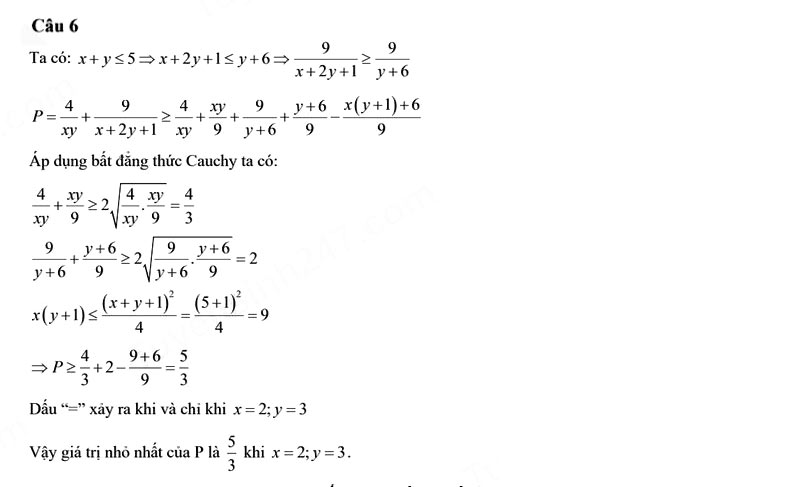

Xem thêm thông tin:
- Tra cứu điểm thi tuyển sinh lớp 10 năm 2024 Hà Nam
- Điểm chuẩn lớp 10 năm 2024 Hà Nam
- Đáp án đề thi tuyển sinh lớp 10 môn Văn Hà Nam 2024
- Đáp án đề thi tuyển sinh lớp 10 môn Anh Hà Nam 2024
Đề thi vào 10 môn Toán tỉnh Hà Nam 2023
ĐỀ THI

ĐÁP ÁN VÀ THANG ĐIỂM CHÍNH THỨC
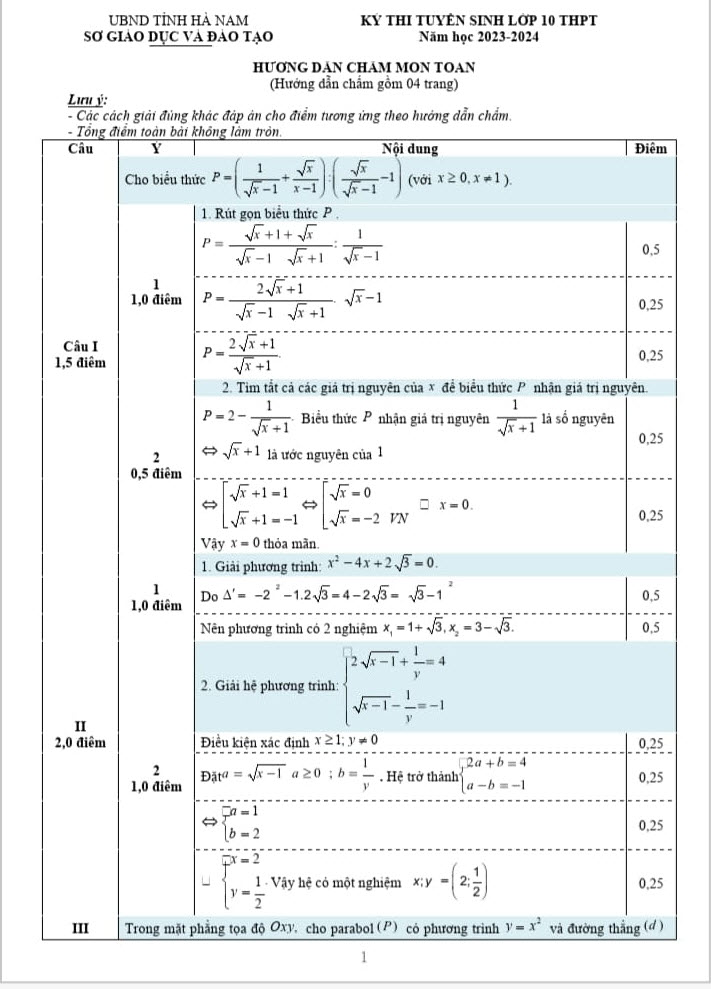

ĐÁP ÁN THAM KHẢO
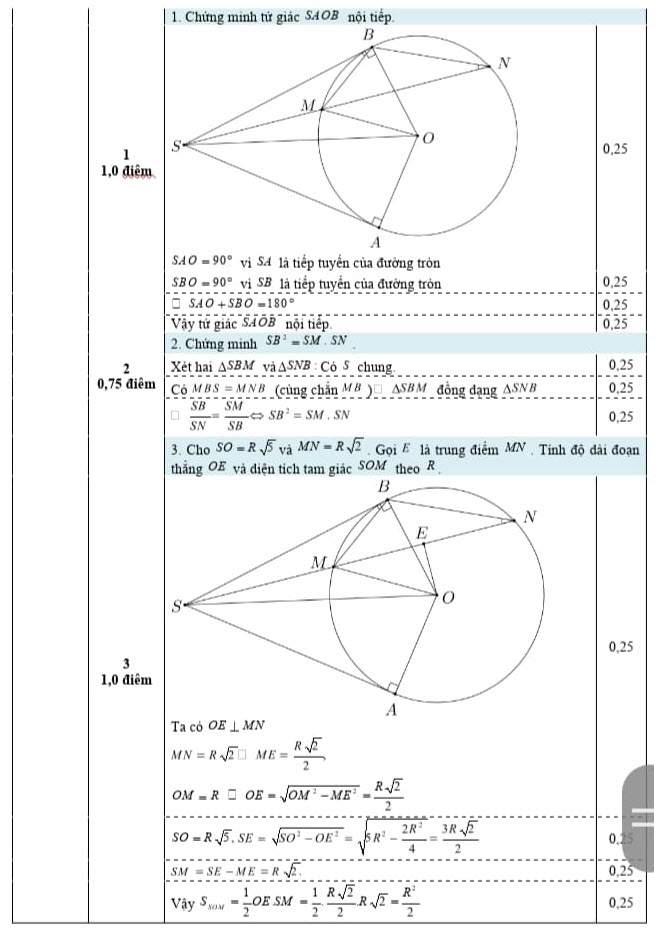
Câu 1.

Câu 2.

Câu 3.

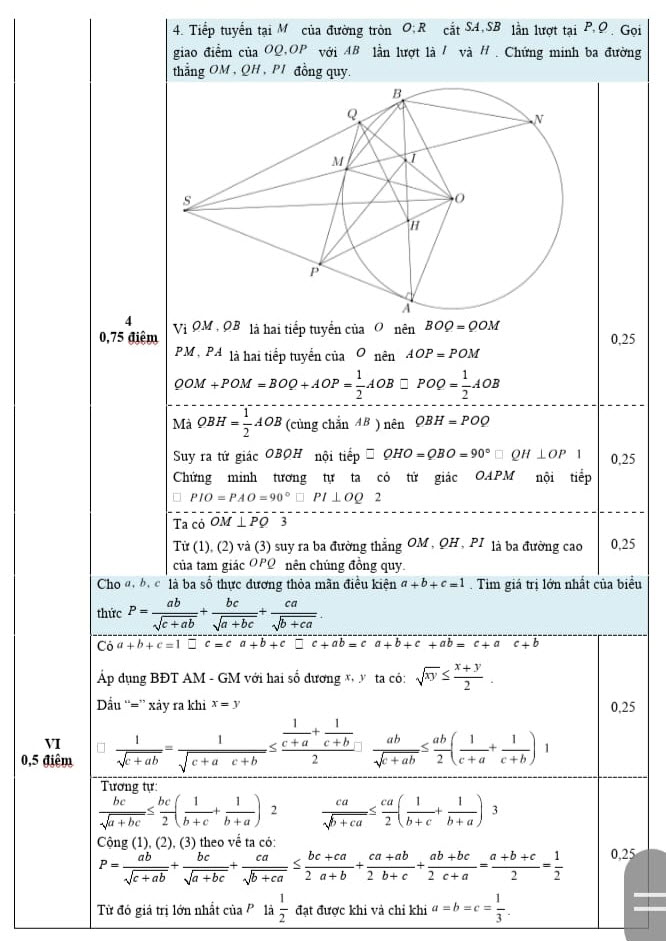
Câu 4.
Đặt x là số tiền điện mà mỗi hộ gia đình bác An dùng trong tháng 4 năm 2023. (500 > x > 65, nghìn đồng).
y là số tiền điện mà mỗi hộ gia đình bác Bình dùng trong tháng 4 năm 2023. (500 > y > 65, nghìn đồng).
Theo đề bài, hai hộ gia đình bác An và bác Bình dùng hết tổng cộng 500 nghìn đồng tiền điện. Vì vậy, ta có phương trình:
x + y = 500 (1)
Sang tháng 5 năm 2023, nhà bác An giảm được 15% tiền điện và nhà bác Bình giảm được 10% tiền điện. Điều này tương đương với việc cả hai hộ gia đình tiết kiệm được tổng cộng 65 nghìn đồng tiền điện so với tháng 4 năm 2023. Ta có phương trình:
0.15x + 0.10y = 65
Kết hợp phương trình (1), ta có:
\( \left\{ \matrix{ x + y = 500 \hfill \cr 0.15x + 0.10y \hfill \cr} \right.⇔ \left\{ \matrix{ x = 300 \hfill \cr y = 200 \hfill \cr} \right.\)
Vậy, ..........
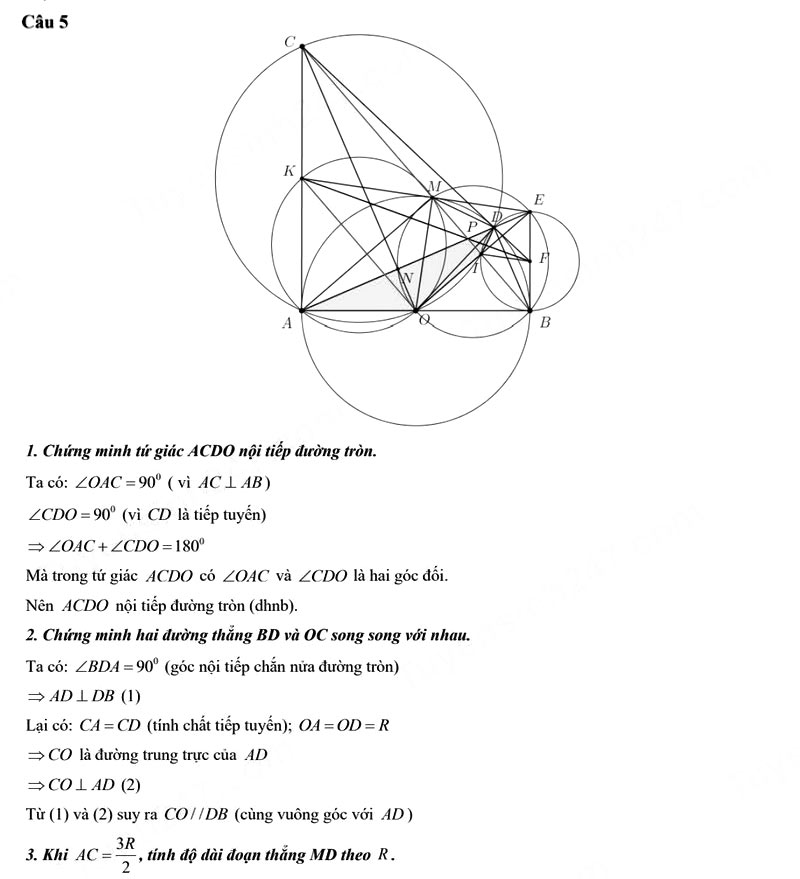
Câu 5.


Câu 6.
\(P=\dfrac{ab}{\sqrt{c+ab}}+\dfrac{bc}{\sqrt{a+bc}}+\dfrac{ca}{\sqrt{b+ca}}\)
Ta có:
\(\sqrt{c+ab} =\sqrt{c\left(a+b+c\right)+ab}=\sqrt{c^2+ac+cb+ab}=\sqrt{\left(c+a\right)\left(c+b\right)}\)
\(\dfrac{ab}{\sqrt{c+ab}}\le\dfrac{ab}{2}\left(\dfrac{1}{c+a}+\dfrac{1}{b+c}\right)\)
tương tự ta có:
\(\dfrac{bc}{\sqrt{a+bc}}\le\dfrac{1}{2}\left(\dfrac{1}{a+b}+\dfrac{1}{a+c}\right);\dfrac{ac}{\sqrt{b+ca}}\le\dfrac{1}{2}\left(\dfrac{1}{b+a}+\dfrac{1}{a+c}\right)\)
\(\Rightarrow P\le\dfrac{bc+ac}{2\left(a+b\right)}+\dfrac{ac+ab}{2\left(a+b\right)}+\dfrac{bc+ab}{2\left(c+b\right)}=\dfrac{1}{2}\left(a+b+c\right)=\dfrac{1}{2}\)
Dấu = xảy ra khi \(a=b=c= \dfrac{1}{3}\)
Đề thi vào 10 môn Toán tỉnh Hà Nam 2022

ĐÁP ÁN
Câu 1:
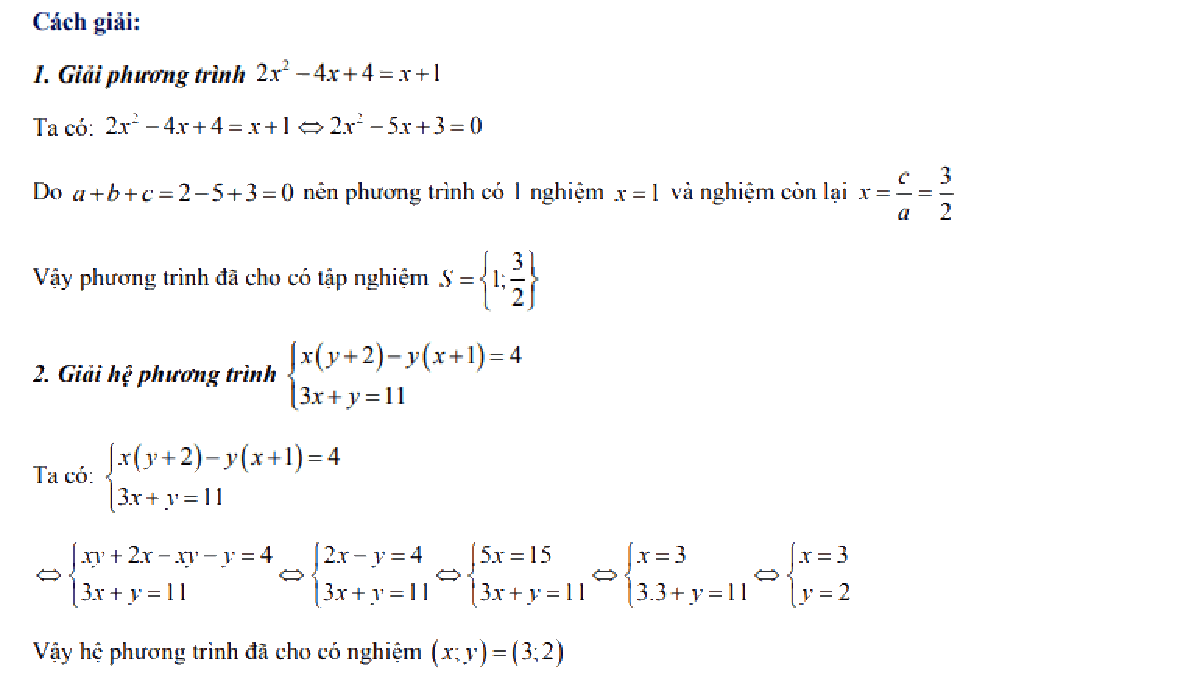
Câu 2:

Câu 3:

Câu 4:

Câu 5:

Câu 6:
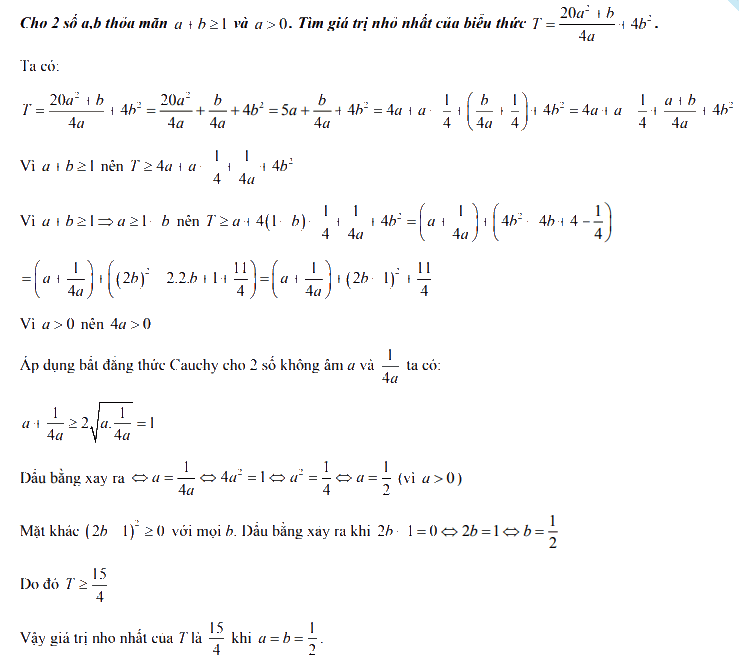
Đề thi vào lớp 10 môn Toán Hà Nam 2021

Đáp án đề thi vào lớp 10 môn Toán Hà Nam 2021
Câu I.
1.
Ta có \(\Delta=7^{2}-4.10=9=3^{2}>0\) nên phương trình đã cho có 2 nghiệm phân biệt
\(\left[\begin{array}{l}x=\frac{-7+3}{2}=-2 \\ x=\frac{-7-3}{2}=-5\end{array}\right..\)
Vậy phương trình đã cho có tập nghiệm S={-5 ;-2}
2.
\(\begin{aligned} &\left\{\begin{array} { l } { 2 ( x - 3 ) = y - 1 } \\ { 3 x + 4 y = 1 3 } \end{array} \Leftrightarrow \left\{\begin{array} { l } { 2 x - 6 + 1 = y } \\ { 3 x + 4 y = 1 3 } \end{array} \Leftrightarrow \left\{\begin{array}{l} y=2 x-5 \\ 3 x+4 y=13 \end{array}\right.\right.\right. \\ &\Leftrightarrow\left\{\begin{array} { l } { 3 x + 4 ( 2 x - 5 ) = 1 3 } \\ { y = 2 x - 5 } \end{array} \Leftrightarrow \left\{\begin{array}{l} 3 x+8 x-20=13 \\ y=2 x-5 \end{array}\right.\right. \\ &\Leftrightarrow\left\{\begin{array} { l } { 1 1 x = 3 3 } \\ { y = 2 x - 5 } \end{array} \Leftrightarrow \left\{\begin{array}{l} x=3 \\ y=1 \end{array}\right.\right. \end{aligned}\)
Vậy hệ phương trình có nghiệm (x, y) = (3 ; 1).
Câu II.
1.
a.
\(\begin{aligned} &A=\frac{1}{2 \sqrt{x}-2}+\frac{1}{2 \sqrt{x}+2}+\frac{1}{x-1} \\ &A=\frac{1}{2(\sqrt{x}-1)}+\frac{1}{2(\sqrt{x}+1)}+\frac{1}{(\sqrt{x}-1)(\sqrt{x}+1)} \\ &A=\frac{\sqrt{x}+1+\sqrt{x}-1+2}{2(\sqrt{x}-1)(\sqrt{x}+1)} \\ &A=\frac{2 \sqrt{x}+2}{2(\sqrt{x}-1)(\sqrt{x}+1)} \\ &A=\frac{2(\sqrt{x}+1)}{2(\sqrt{x}-1)(\sqrt{x}+1)} \\ &A=\frac{1}{\sqrt{x}-1} \\ &\text { Vậy với } x \geq 0, x \neq 1 \text { thì } A=\frac{1}{\sqrt{x}-1} \text { . } \end{aligned}\)
b.
Để \(A \in \mathbb{Z}\) thì \(\dfrac{1}{\sqrt{x}-1} \in \mathbb{Z}\), mà \(x \in \mathbb{Z}\) nên \(\sqrt{x}-1 \in U(1)=\{-1 ; 1\}.\)
TH1: \(\sqrt{x}-1=1 \Leftrightarrow \sqrt{x}=2 \Leftrightarrow x=4(t m).\)
TH2: \(\sqrt{x}-1=-1 \Leftrightarrow \sqrt{x}=0 \Leftrightarrow x=0(\mathrm{tm}).\)
Vậy để \(A \in \mathbb{Z}\,\, thì\,\,x \in{0 ; 4}.\)
2.
Gọi chiều dài và chiều rộng của mảnh vườn lần lượt là x, y(m) (ĐK: x, y>0 ).
Vì diện tích mảnh vườn là 680 m² nên ta có phương trình xy=680 (1).
Khi tăng chiều dài thêm 6 m và giảm chiều rộng đi 3 m thì chiều dài mới của mảnh vườn là x+6 (m) và chiều rộng mới của mảnh vườn là y-3 (m).
Vì diện tích mảnh vườn lúc sau không đổi nên ta có phương trình (x+6)(y-3)=680 (2)
Từ (1) và (2) ta có hệ phương trình
\(\left\{\begin{array}{l}x y=680 \\ (x+6)(y-3)=680\end{array}\right.\)
\(\begin{aligned} &\Leftrightarrow\left\{\begin{array} { l } { x y = 6 8 0 } \\ { x y - 3 x + 6 y - 1 8 = 6 8 0 } \end{array} \Leftrightarrow \left\{\begin{array}{l} x y=680 \\ 680-3 x+6 y-18=680 \end{array}\right.\right. \\ &\Leftrightarrow\left\{\begin{array} { l } { x y = 6 8 0 } \\ { 3 x - 6 y + 1 8 = 0 } \end{array} \Leftrightarrow \left\{\begin{array} { l } { x y = 6 8 0 } \\ { x - 2 y = - 6 } \end{array} \Leftrightarrow \left\{\begin{array}{l} x y=680 \\ x=2 y-6 \end{array}\right.\right.\right. \\ &\Leftrightarrow\left\{\begin{array} { l } { ( 2 y - 6 ) y = 6 8 0 } \\ { x = 2 y - 6 } \end{array} \Leftrightarrow \left\{\begin{array} { l } { 2 y ^ { 2 } - 6 y - 6 8 0 = 0 } \\ { x = 2 y - 6 } \end{array} \Leftrightarrow \left\{\begin{array}{l} y^{2}-3 y-340=0(*) \\ x=2 y-6 \end{array}\right.\right.\right. \end{aligned}\)
Phương trình (*) có \(\Delta=(-3)^{2}-4 .(-340)=1396=37^{2}>0\) nên phương trình (*) có 2 nghiệm phân biệt
\(\left[\begin{array}{l} y=\dfrac{3+37}{2}=20(\mathrm{tm}) \\ y=\dfrac{3-37}{2}=-17 \mathrm{(ktm}) \end{array}\right.\)
Với \(y=20 \Rightarrow x=2.20-6=34(\mathrm{tm}).\)
Vậy chiều dài và chiều rộng của mảnh vườn lần lượt là 34 m và 20 m nên chu vi của mành vườn ban đầu là C=2 .(34+20)=108(m).
Câu III.
1.
Ta có các điểm thuộc parabol (P) có tung độ bằng 9 thỏa mãn:
\(x^{2}=9 \Leftrightarrow\left[\begin{array}{l}x=3 \\ x=-3\end{array}\right.\)
Vậy các điểm cần tìm là (3 ; 9) và (-3 ; 9).
2.
Xét phương trình hoành độ giao điểm của (d) và (P) ta có:
\(x^{2}-2(m-1) x-m^{2}-2 m=0\)
Ta có: \(\Delta^{\prime}=(m-1)^{2}-\left(-m^{2}-2 m\right)=m^{2}-2 m+1+m^{2}+2 m=2 m^{2}+1>0 \forall m.\)
Do đó đường thẳng (d) luôn cắt (P) tại hai điểm phân biệt A, B.
Ta gọi hai điểm phân biệt đó là điểm \(A\left(x_{1}, y_{1}\right)\) và \(B\left(x_{2}, y_{2}\right).\)
\(\begin{aligned} &\text { Mà } A, B \in(P) \text { nên }\left\{\begin{array}{l} y_{1}=x_{1}^{2} \\ y_{2}=x_{2}^{2} \end{array}\right.\\ &\text { Theo hệ thức Vi-ét ta có: }\left\{\begin{array}{l} x_{1}+x_{2}=-\frac{b}{a}=2(m-1) \\ x_{1} x_{2}=\frac{c}{a}=-m^{2}-2 m \end{array}\right.\\ &\text { Khi đó ta có: } y_{1}+y_{2}=4 \end{aligned}\)
\(\begin{aligned} &\Leftrightarrow x_{1}^{2}+x_{2}^{2}=4 \\ &\Leftrightarrow\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}=4 \\ &\Rightarrow 4(m-1)^{2}-2\left(-m^{2}-2 m\right)=4 \\ &\Leftrightarrow 4 m^{2}-8 m+4+2 m^{2}+4 m-4=0 \\ &\Leftrightarrow 6 m^{2}-4 m=0 \\ &\Leftrightarrow 2 m(3 m-2)=0 \\ &\Leftrightarrow\left[\begin{array}{l} m=0 \\ m=\dfrac{2}{3} \end{array}\right. \end{aligned}\)
Vậy tập các giá trị của m thỏa mẫn là \(\left\{0 ; \dfrac{2}{3}\right\}\).
Câu IV.
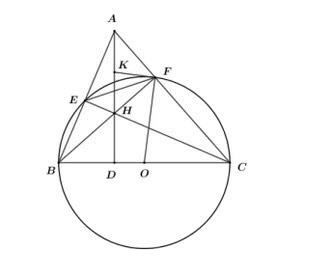
1.
Ta có ∠BEC = ∠BFC = 90⁰ (góc nội tiếp chắn nửa đường tròn) nên ∠AEH=∠AFH=90⁰.
Xét tứ giác AEHF có: ∠AEH+∠AFH=90⁰+90⁰=180⁰.
Mà 2 góc này nằm ở vị trí hai góc đối diện của tứ giác AEHF nên AEHF là tứ giác nội tiếp (dhnb).
2.
Vì BCFE là tứ giác nội tiếp đường tròn (O) nên ∠AEF=∠ACB (góc ngoài và góc trong tại đình đối diện của tứ giác nội tiếp).
Xét △AEF và △ACB có: ∠BAC chung; ∠AEF=∠ACB(cmt)
\(\Rightarrow \Delta AEF \sim \Delta ACB(g.g) \Rightarrow \dfrac{A E}{A C}=\dfrac{A F}{A B} \Rightarrow A F \cdot A C=A E . A B \)(đpcm).

Cùng ôn tập chuẩn bị thật tốt cho kỳ thi sắp tới với đề thi tuyển sinh lớp 10 các năm trước nhé:
Tuyển tập đề thi tuyển sinh lớp 10 Hà Nam môn Toán qua các năm
Đề thi vào 10 môn Toán Hà Nam năm 2020

Xem chi tiết đề thi và đáp án tại link: Đề thi môn Toán vào lớp 10 Hà Nam 2020 (có lời giải)
Đề thi vào 10 môn Toán Hà Nam năm 2019
Câu I. (2,0 điểm)
1) Giải phương trình: \(x^2-5x+4=0\)
2) Giải hệ phương trình: \(\left\{\begin{array}{l} 3 x-y=3 \\ 2 x+y=7 \end{array}\right.\)
Xem chi tiết đề thi và đáp án tại link: Đề thi vào lớp 10 môn Toán tỉnh Hà Nam năm 2019
Đề thi vào 10 môn Toán Hà Nam năm 2018
Câu 1. (2,0 điểm)
1) Giải phương trình: \(x^2+6x+5=0\)
2) Giải hệ phương trình \(\left\{\begin{array}{l} x+y=25 \\ 2 x-1=y+4 \end{array}\right.\)
Xem chi tiết đề thi và đáp án tại link: Đề thi vào lớp 10 môn toán tỉnh Hà Nam 2018
Trên đây là toàn bộ nội dung của đề thi tuyển sinh lớp 10 môn Toán 2023 và các năm trước mà Đọc Tài Liệu chia sẻ nhằm giúp các em nắm được các thông tin về kỳ thi này.
Mong rằng những tài liệu của chúng tôi sẽ là người đồng hành giúp các bạn hoàn thành tốt bài thi của mình.
Xem thêm: Điểm thi tuyển sinh lớp 10 năm 2023
