NEW: Đề thi vào 10 môn Toán tỉnh Hà Nam 2021-2022
Đáp án đề thi vào lớp 10 môn Toán năm học 2020/2021 của tỉnh Hà Nam được ĐọcTàiLiệu cập nhật giúp các em học sinh tham khảo, so sánh kết quả với bài thi của mình.
Đề thi vào lớp 10 năm 2020
Chi tiết đề thi vào lớp môn Toán của Hà Nam như sau:
Sở GD&ĐT Hà Nam ĐỀ CHÍNH THỨC | KỲ THI TUYỂN SINH VÀO LỚP 10 NĂM HỌC: 2020 - 2021 Môn: Toán Thời gian làm bài: 120 phút |

(Thông tin được cập nhật chính thức đối với kỳ thi tuyển sinh lớp 10 năm học 2020/2021 của tỉnh Hà Nam)
Đáp án đề thi môn Toán vào lớp 10 Hà Nam 2020
Dự kiến: Đáp án đề thi tuyển sinh vào 10 môn Toán Hà Nam năm 2020 sẽ được cập nhật sau khi kết thúc thời gian thi chính thức 30 - 40 phút
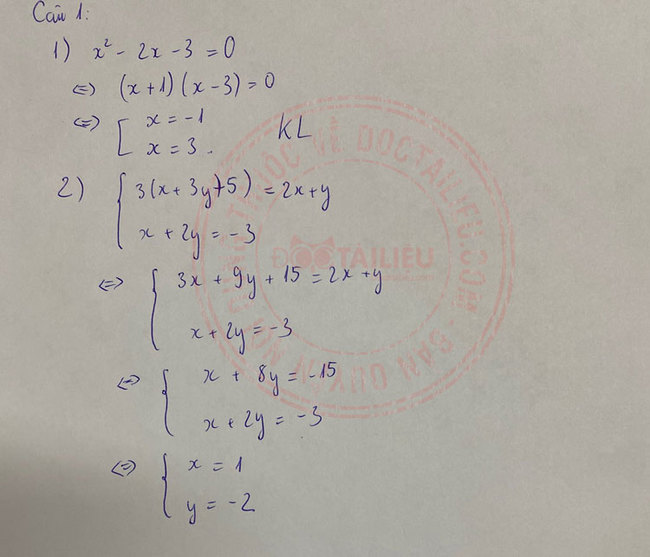
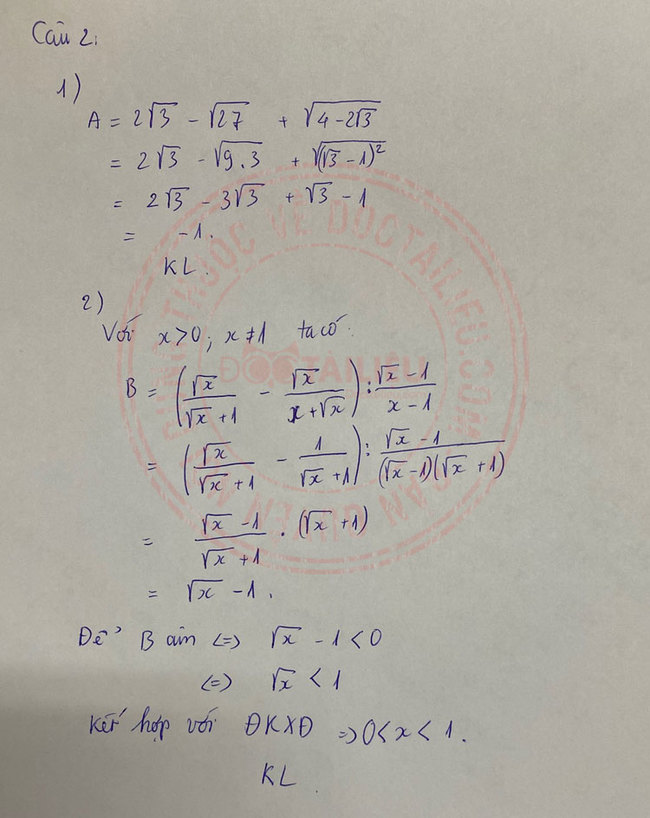

Câu 4:
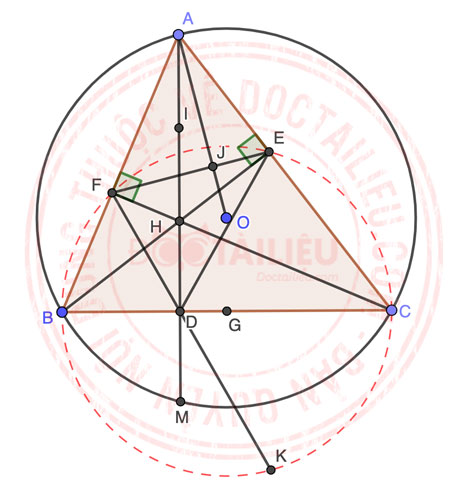
1)
Vì BE, CF là đường cao của △ABC ⇒ ∠AFH = ∠AEH = 90° ⇒ Tứ giác AEHF nội tiếp đường tròn đường kính AH (đpcm).
2)
Vì tứ giác AEHF nội tiếp ⇒ ∠MBC = ∠MAC = ∠HAE = 90° - ∠AHE = 90° - ∠BHD = ∠HBD
Hay BC là phân giác của góc MBE (đpcm).
3)
Vì Tứ giác AEHF nội tiếp đường tròn đường kính AH (cmt), có I là tâm ngoại tiếp ⇒ I là trung điểm AH.
Gọi G là trung điểm BC.
Dễ thấy △BEC vuông tại E có EG là trung tuyến ⇒ GB = GE = GC ⇒ G là tâm đường tròn ngoại tiếp △BEC.
Ta có:
∠IEG = ∠IEH + ∠BEG = 90° - ∠IEA + 90° - ∠GEC = 180° - ∠IAE - ∠GCE
= 180° - ∠DAC - ∠DCA = 90°
Hay IE ⊥ EG hay IE là tiếp tuyến của đường tròn ngoại tiếp △BEC (đpcm).
4)
Vì ∠BFC = ∠BEC = 90° ⇒ Tứ giác BFEC nội tiếp ⇒ ∠FBC + ∠FEC = 180°
⇒ ∠ABC = ∠FBC = 180° - ∠FEC = ∠FEA
Gọi OA cắt EF tại J.
Ta có: ∠AJE = 180° - ∠JAE - ∠JEA = 180° - ∠OAC - ∠FEA
\(= 180° - \dfrac{180° - ∠AOC}2 - ∠ABC = 90° + ∠ABC - ∠ABC = 90°\)
⇒ AJ ⊥ JE hay AO ⊥ EF (đpcm).
Kéo dài FD cắt đường tròn ngoại tiếp △BEC tại K.
Ta thấy:
∠KDC = ∠BDF (đối đỉnh) = ∠BHF (góc nội tiếp) = ∠CHE (đối đỉnh)= ∠CDE (góc nội tiếp)
⇒ DC là phân giác góc KDE.
⇒ K là điểm đối xứng của E qua BC ⇒ DK = DE
⇒ FD + DE = FD + DK = FK ≤ 2r = BC.
Ta lại có:
△AEF ∽ △ABC ⇒ \(\dfrac{EF}{AE} = \dfrac{BC}{AB}\) ⇒ \(EF = \dfrac{AE.BC}{AB} = BC.cos∠BAE = BC.cos\dfrac{∠BOC}2 = BC.\dfrac{OG}{OB} = const\)
(do B,C,O cố định)
Ta có:
\(EF + FD + DE = EF + FK \leq \dfrac{BC.OG}{OB} + BC\)
Vậy \(Max_{EF + FD + DE}= \dfrac{BC.OG}{OB} + BC = const ⇔ FK = BC \)
hay △ABC cân tại A.

-/-
Môn thi trước đó: Đáp án đề thi vào lớp 10 môn Văn Hà Nam năm 2020
Trên đây là toàn bộ nội dung của đáp án đề thi tuyển sinh vào lớp 10 môn Toán năm 2020 của Hà Nam được Đọc Tài Liệu thực hiện sau khi kì thi chính thức diễn ra. Với nội dung này các em có thể so sánh đối chiếu kết quả bài thi của mình!
Mong rằng đáp án đề thi môn Toán vào lớp 10 Hà Nam 2020 của chúng tôi sẽ là người đồng hành hữu ích với bạn trong kỳ thi này.
