Đề thi tuyển sinh vào lớp 10 môn Toán năm 2022 chính thức của Sở Giáo dục và Đào Tạo tỉnh Nam Định được cập nhật nhanh nhất. Cùng Đọc tài liệu tham khảo ngay.
Đề thi vào 10 môn Toán Nam Định 2023
Đề thi sẽ được cập nhật chính thức khi kỳ thi tuyển sinh vào lớp 10 của tỉnh diễn ra, vì vậy đáp án đề thi vào lớp 10 môn toán Nam Định sẽ được cập nhật sau khi kết thúc thời gian thi.
ĐỀ THI


HƯỚNG DẪN CHẤM
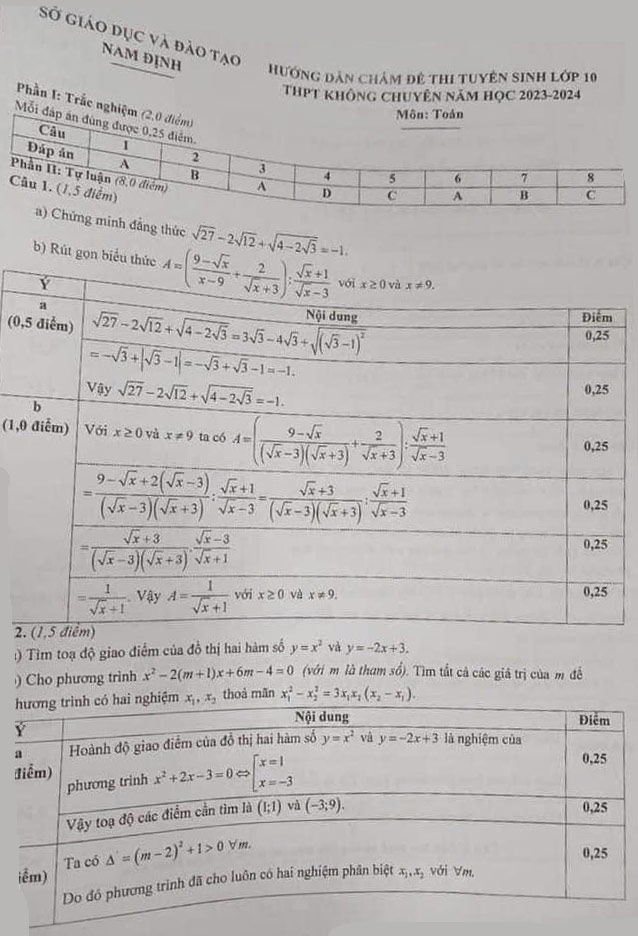



TRẮC NGHIỆM
1. A
2. B
3. A
4. D
5. C
6. A
7. B
8. C
II,. TỰ LUẬN




Câu 5.

Xem thêm
- Chỉ tiêu tuyển sinh vào lớp 10 Nam Định
- Điểm chuẩn lớp 10 năm 2023 Nam Định
- Điểm thi tuyển sinh lớp 10 năm 2023 Nam Định
- Đề thi tiếng Anh vào lớp 10 tỉnh Nam Định 2023
- Đề thi vào lớp 10 môn Văn Nam Định 2023
Đề thi tuyển sinh lớp 10 môn toán Nam Định 2022
Đề thi


TRẮC NGHIỆM
1 - C
2 - B
3 - A
4 - C
5 - C
6 - A
7 - B
8 - D
TỰ LUẬN
Câu 1

Câu 2

Câu 3

Câu 4

2.

Câu 5.

Đề thi vào lớp 10 môn Toán Nam Định 2021
Đề thi vào lớp 10 môn Toán năm 2021 tỉnh Nam Định chính thức của các trường THPT công lập sẽ được cập nhật ngay khi kỳ thi diễn ra ngày 28/7/2021.


Đáp án đề thi vào 10 môn Toán Nam Định 2021
Phần 1. Trắc nghiệm
|
1. A 2. D 3. A 4. C |
5. C 6. B 7. C 8. B |
Phần 2. Tự luận
Câu 1.
1.
\(\left(2-\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\right) \cdot\left(2+\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\right)=\left(2-\dfrac{\sqrt{3}(\sqrt{3}+1)}{\sqrt{3}+1}\right) \cdot\left(2+\dfrac{\sqrt{3}(\sqrt{3}-1)}{\sqrt{3}-1}\right)\)
\(= (2 - \sqrt{3})(2+ \sqrt{3}) = 2^2- (\sqrt{3})^2 = 4 - 3 = 1 => ĐPCM\)
2.
\(A=\left(\dfrac{1}{x-2 \sqrt{x}}+\dfrac{1}{\sqrt{x}-2}\right): \dfrac{\sqrt{x}+1}{x-4 \sqrt{x}+4} \text { với } x>0 ; x \neq 4\)
\(=\left(\dfrac{1}{\sqrt{x}(\sqrt{x}-2)}+\dfrac{1}{\sqrt{x}-2}\right): \dfrac{\sqrt{x}+1}{(\sqrt{x}-2)^2} \)
\(=\left(\dfrac{1}{\sqrt{x}(\sqrt{x}-2)}+\dfrac{\sqrt{x}}{\sqrt{x}(\sqrt{x}-2)}\right): \dfrac{\sqrt{x}+1}{(\sqrt{x}-2)^2} \)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}(\sqrt{x}-2)}: \dfrac{\sqrt{x}+1}{(\sqrt{x}-2)^2} \)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}(\sqrt{x}-2)}. \dfrac{(\sqrt{x}-2)^2}{\sqrt{x}+1} \)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
KL: ....
Câu 2.
1.
Tọa độ của tất cả các điểm thuộc parabol có tung độ bằng -8 là nghiệm của phương trình:
\(-2 x^{2}=-8 \Leftrightarrow x^{2}=4 \Leftrightarrow\left[\begin{array}{l} x=2 \\ x=-2 \end{array}\right.\)
Vậy các điểm cần tìm là A(2 ;-8) và B(-2 ;-8).
2.
Phương trình có hai nghiệm phân biệt \(\Leftrightarrow \Delta^{\prime}>0\)
\(\Rightarrow(m+1)^{2}-m^{2}-2 m=m^{2}+2 m+1-m^{2}-2 m=1>0 \quad \forall m .\)
Do đó phương trình đã cho luôn có hai nghiệm phân biệt \(x_{1}, x_{2}\) với mọi m.
Áp dụng hệ thức Vi-ét ta có:
\(\left\{\begin{array}{l}x_{1}+x_{2}=-\dfrac{b}{a}=2(m+1)=2 m+2 \\ x_{1} \cdot x_{2}=\dfrac{c}{a}=m^{2}+2 m\end{array}\right.\)
Theo bài ra ta có:
\(\left|x_{1}\right|=3\left|x_{2}\right| \Rightarrow x_{1}^{2}=9 x_{2}^{2} \Rightarrow x_{1}^{2}-9 x_{2}^{2}=0 \Rightarrow\left(x_{1}-3 x_{2}\right)\left(x_{1}+3 x_{2}\right)=0\)
TH1:\( x_{1}-3 x_{2}=0 \Rightarrow x_{1}=3 x_{2}.\)
Thay vào (1) ta có:
\(\left\{\begin{array}{l}3 x_{2}+x_{2}=2 m+2 \\ 3 x_{2}^{2}=m^{2}+2 m\end{array} \Leftrightarrow\left\{\begin{array}{l}x_{2}=\dfrac{2 m+2}{4}=\dfrac{m+1}{2} \\ 3 \cdot\left(\dfrac{m+1}{2}\right)^{2}=m^{2}+2 m\end{array} \Leftrightarrow\left\{\begin{array}{l}x_{2}=\dfrac{m+1}{2} \\ \dfrac{3}{4} \cdot\left(m^{2}+2 m+1\right)-m^{2}-2 m=0\end{array}\right.\right.\right.\)
\(\Leftrightarrow\left\{\begin{array}{l}x_{2}=\dfrac{m+1}{2} \\ -\dfrac{1}{4} m^{2}-\dfrac{1}{2} m+\dfrac{3}{4}=0\end{array} \Leftrightarrow\left\{\begin{array}{l}x_{2}=\dfrac{m+1}{2} \\ m^{2}+2 m-3=0(*)\end{array}\right.\right.\)
Phương trình \(\left(^{*}\right) có a+b+c=1+2+(-3)=0\) nên phương trình có 2 nghiệm phân biệt \(\left[\begin{array}{l}m=1 \\ m=-3\end{array}\right..\)
Với \(m=1 \Rightarrow\left\{\begin{array}{l}x_{2}=1 \\ x_{1}=3 x_{2}=3\end{array}(\mathrm{ktm})\right..\)
Với \(m=-3 \Rightarrow\left\{\begin{array}{l}x_{2}=-1 \\ x_{1}=3 x_{2}=-3\end{array}(\mathrm{tm})\right..\)
TH2: \(x_{1}=-3 x_{2}\)
Thay vào (1) ta có:
\(\left\{\begin{array}{l}-3 x_{2}+x_{2}=2 m+2 \\ -3 x_{2}^{2}=m^{2}+2 m\end{array} \Leftrightarrow\left\{\begin{array}{l}x_{2}=-m-1 \\ -3(-m-1)^{2}=m^{2}+2 m\end{array}\right.\right.\)
\(\Leftrightarrow\left\{\begin{array}{l}x_{2}=-m-1 \\ 3\left(m^{2}+2 m+1\right)+m^{2}+2 m=0\end{array} \Leftrightarrow\left\{\begin{array}{l}x_{2}=-m-1 \\ 4 m^{2}+8 m+3=0(* *)\end{array}\right.\right.\)
Phương trình (**) có \( \Delta^{\prime}=4^{2}-4.3=4=2^{2}>0\) nên phương trình (**) có 2 nghiệm phân biệt là
\(\left[\begin{array}{l}m=\dfrac{-4+2}{4}=-\dfrac{1}{2} \\ m=\dfrac{-4-2}{4}=-\dfrac{3}{2}\end{array}\right.\)
Với \(m=-\dfrac{1}{2} \Rightarrow\left\{\begin{array}{l}x_{2}=-\dfrac{1}{2} \\ x_{1}=-3 x_{2}=\dfrac{3}{2}\end{array}(\mathrm{ktm})\right.\)
Với \(m=-\dfrac{3}{2} \Rightarrow\left\{\begin{array}{l}x_{2}=\dfrac{1}{2} \\ x_{1}=-3 x_{2}=-\dfrac{3}{2}\end{array}(t m)\right.\)
Vậy tập các giá trị m thỏa mãn yêu cầu bài toán là \(S=\left\{-3 ;-\dfrac{3}{2}\right\}.\)
Câu 3.
ĐKXĐ: \(x \neq 0, y \neq 0\).
Ta đặt
\(\left\{\begin{array}{l}\dfrac{x}{y}+2 \cdot \dfrac{y}{x}=3 \\ 2 x^{2}-3 y=-1\end{array}\right.\)
Xét phương trình (1): \(\dfrac{x}{y}+2 \dfrac{y}{x}=3.\)
Đặt \(t=\dfrac{x}{y}(t \neq 0)\), phương trình (1) trở thành \(t+2 \cdot \dfrac{1}{t}=3 \Rightarrow t^{2}-3 t+2=0 \,(1')\)
Vì a+b+c=1+(-3)+2=0 nên phương trình (1') có 2 nghiệm phân biệt
\(\left[\begin{array}{l}t=1 \\ t=\dfrac{c}{a}=2\end{array}(\mathrm{tm})\right..\)
+) TH1: t = 1 \(\Rightarrow \dfrac{x}{y}=1 \Leftrightarrow x=y.\)
Thế vào phương trình (2) ta có: \(2 x^{2}-3 x=-1 \Leftrightarrow 2 x^{2}-3 x+1=0 (2')\)
Vì a+b+c=2+(-3)+1=0 nên phương trình (2') có 2 nghiệm phân biệt
\(\left[\begin{array}{l}x=1 \Rightarrow y=1 \\ x=\dfrac{c}{a}=\dfrac{1}{2} \Rightarrow y=\dfrac{1}{2}(t m) \text { . }\end{array}\right.\)
+) TH2: \(t=2 \Rightarrow \dfrac{x}{y}=2 \Leftrightarrow x=2 y.\)
Thế vào phương trình (2) ta có: 2. \((2 y)^{2}-3 y=-1 \Leftrightarrow 8 y^{2}-3 y+1=0 (2")\)
Ta có \(\Delta=(-3)^{2}-4.8 .1=-23<0\) nên phương trình (2") vô nghiệm).
Vậy hệ phương trình đã cho có nghiệm \((x ; y) \in\left\{(1 ; 1) ;\left(\dfrac{1}{2} ; \dfrac{1}{2}\right)\right\}\)
Câu 4.
1.
Diện tích hình chữ nhật ABCD là
\(S=A B \cdot B C=6.4=24\left(m^{2}\right).\)
Diện tích nửa hình tròn đường kính AB và nửa hình tròn đường kính CD bằng nhau và bằng
\(S^{\prime}=\dfrac{1}{2} \pi \cdot\left(\dfrac{A D}{2}\right)^{2}=\dfrac{1}{2} \pi \cdot\left(\dfrac{4}{2}\right)^{2}=2 \pi\left(m^{2}\right)\)
=> Diện tích phần đất trồng hoa là \(S_{1}=2 S^{\prime}=4 \pi\left(m^{2}\right)\).
Vậy diện tích phần đất để trồng cỏ là \(S_{2}=S-S_{1}=24-4 \pi \approx 11,4\left(m^{2}\right).\)
2.

Câu 5.
1.
\(4 x+1-\sqrt{9(2 x-1)(x+1)}+2 \sqrt{2 x-1}-2 \sqrt{x+1}=0\)
Điều kiện xác định: \(x \geq \dfrac{1}{2}\)
\(Đặt \sqrt{2 x-1}=a, \sqrt{x+1}=b(a \geq 0, b \geq 0)\)
\(Suy ra 4 x+1=2 x-1+2(x+1)=a^{2}+2 b\)
Phương trình ban đầu trở thành:
\(a^{2}+2 b^{2}-3 a b+2 a-2 b=0\)
\(\Leftrightarrow\left(a^{2}-2 a b+b^{2}\right)+\left(b^{2}-a b\right)+(2 a-2 b)=0\)
\(\Leftrightarrow(a-b)^{2}+b(b-a)+2(a-b)=0\)
\(\Leftrightarrow(a-b)^{2}-b(a-b)+2(a-b)=0\)
\(\Leftrightarrow(a-b)(a-b-b+2)=0\)
\(\Leftrightarrow(a-b)(a-2 b+2)=0\)
\(\Leftrightarrow\left[\begin{array}{l}a=b \\ a-2 b+2=0\end{array}\right.\)
TH1: \(a=b \Rightarrow \sqrt{2 x-1}=\sqrt{x+1} \Leftrightarrow 2 x-1=x+1 \Leftrightarrow x=2 (TMĐK)\)
TH2: \(a-2 b+2=0 \Leftrightarrow \sqrt{2 x-1}-2 \sqrt{x+1}+2=0\)
\(\Leftrightarrow \sqrt{2 x-1}+2=2 \sqrt{x+1}\)
\(\Leftrightarrow 2 x-1+4+4 \sqrt{2 x-1}=4(x+1)\)
\(\Leftrightarrow 2 x+1=4 \sqrt{2 x-1}\)
\(\Leftrightarrow(2 x+1)^{2}=16(2 x-1)\left(\right. do \left.x \geq \dfrac{1}{2}\right)\)
\(\Leftrightarrow 4 x^{2}+4 x+1-32 x+16=0\)
\(\Leftrightarrow 4 x^{2}-28 x+17=0\)
Ta có: \(\Delta^{\prime}=14^{2}-4.17=128>0\)
Phương trình có hai nghiệm phân biệt:
\(\left[\begin{array}{l} x_{1}=\dfrac{-b^{\prime}+\sqrt{\Delta}}{a}=\dfrac{14+8 \sqrt{2}}{4}=\dfrac{7+4 \sqrt{2}}{2} \\ x_{2}=\dfrac{-b^{\prime}-\sqrt{\Delta}}{a}=\dfrac{14-8 \sqrt{2}}{4}=\dfrac{7-4 \sqrt{2}}{2} \end{array}\right. \text { (TMĐK). }\\\)
Vậy tập nghiệm của phương trình là: \(S=\left\{2 ; \dfrac{14+\sqrt{128}}{4} ; \dfrac{14-\sqrt{128}}{4}\right\}\) .
2. a, b, c dương thỏa mãn a + b + c = 3
\(P=\dfrac{2021}{\sqrt{a b}+\sqrt{c b}+\sqrt{a c}}-\dfrac{b \sqrt{a}}{1-b}-\dfrac{c \sqrt{b}}{1+c}-\dfrac{a \sqrt{c}}{1+a}\)
Áp dụng BĐT Cauchy - Schwarz ta có: \(\sqrt{a b}+\sqrt{b c}+\sqrt{c a} \leq a+b+c.\)
\(\Rightarrow 0 \leq \sqrt{a b}+\sqrt{b c}+\sqrt{c a} \leq 3 .\)
Áp dụng BĐT AM - GM ta có: \(b+1 \geq 2 \sqrt{b} \Rightarrow \dfrac{b \sqrt{a}}{b+1} \leq \dfrac{\sqrt{a b}}{2}.\)
Tương tự ta có: \(\dfrac{c \sqrt{b}}{1+c} \leq \dfrac{\sqrt{b c}}{2}, \dfrac{a \sqrt{c}}{1+a} \leq \dfrac{\sqrt{c a}}{2}.\)
Khi đó ta có:
\(P \geq \dfrac{2021}{\sqrt{a b}+\sqrt{b c}+\sqrt{c a}}-\dfrac{\sqrt{a b}+\sqrt{b c}+\sqrt{c a}}{2}\)
\(\Rightarrow P \geq\left[\dfrac{2021}{\sqrt{a b}+\sqrt{b c}+\sqrt{c a}}+\dfrac{(\sqrt{a b}+\sqrt{b c}+\sqrt{c a}) \cdot 2021}{9}\right]-\dfrac{4051}{18}(\sqrt{a b}+\sqrt{b c}+\sqrt{c a})\)
\(\Rightarrow P \geq 2 \sqrt{2021 \cdot \dfrac{2021}{9}}-\dfrac{4051}{18} \cdot 3\)
\(\Rightarrow P \geq-\dfrac{1349}{2}\)
Dấu "=" xảy ra khi và chỉ khi a = b = c = 1.
-/-
Cùng ôn tập chuẩn bị thật tốt cho kỳ thi sắp tới với đề thi tuyển sinh lớp 10 các năm trước nhé:
Đề thi vào 10 môn Toán Nam Định năm 2020
Phần II. Tự luận (8,0 điểm)
Bài 1 (1,5 điểm)
- Chứng minh đẳng thức \(\sqrt{(\sqrt{5}-4)^{2}}-\sqrt{5}+\sqrt{20}=4\)
- Rút gọn biểu thức: \(P=\left(\frac{1}{\sqrt{x}+2}+\frac{1}{\sqrt{x}-2}\right): \frac{2}{x-2 \sqrt{x}}\) ( với \( x>0 ; x \neq 4\) )
Xem chi tiết đề thi và đáp án tại link: Đề thi vào lớp 10 môn Toán Nam Định 2020 (có lời giải chi tiết)
Đề thi vào 10 môn Toán Nam Định năm 2019
Trích dẫn đề thi
Câu 4. (3,0 điểm)
Qua điểm A nằm ngoài đường tròn (O) vẽ hai tiếp tuyến AB, AC của đường tròn (B, C là hai tiếp điểm). Gọi E là trung điểm của đoạn AC, F là giao điểm thứ hai của EB với đường tròn (O).
a) Chứng minh: tứ giác ABOC là tứ giác nội tiếp, tam giác CEF đồng dạng với tam giác BEC
b) Gọi K là giao điểm thứ hai của đường thẳng AF với đường tròn (O). Chứng minh BF.CK = BK.CF
c) Chứng minh AE là tiếp tuyến của đường tròn ngoại tiếp tam giác ABF.
Xem chi tiết đề thi và đáp án tại link: Đề thi vào lớp 10 môn Toán tỉnh Nam Định năm 2019 có đáp án
Đề thi vào 10 môn Toán Nam Định năm 2018
Câu 1. (1,5 điểm) Cho biểu thức \(M=\left(\frac{4 x}{\sqrt{x}-1}-\frac{\sqrt{x}-2}{x-3 \sqrt{x}+2}\right) \cdot \frac{\sqrt{x}-1}{x}\) (với x>0; \(x \neq 1\) ; \(x \neq 4\) )
a) Rút gọn biểu thức M
b) Tìm các giá trị x để M<4
Xem chi tiết đề thi và đáp án tại link: Đáp án đề thi môn toán vào lớp 10 tỉnh Nam Định 2018
Trên đây là toàn bộ nội dung của đề thi tuyển sinh lớp 10 môn Toán 2023 và các năm trước mà Đọc Tài Liệu chia sẻ nhằm giúp các em nắm được các thông tin về kỳ thi này.
Mong rằng những tài liệu của chúng tôi sẽ là người đồng hành giúp các bạn hoàn thành tốt bài thi của mình. Tra cứu điểm thi tuyển sinh lớp 10 năm 2023 tại đây!
