Đề thi tuyển sinh vào lớp 10 môn Toán năm 2020 Chuyên Sư Phạm và đáp án được ĐọcTàiLiệu cập nhật giúp các em học sinh tham khảo, so sánh kết quả với bài thi của mình.
Đề thi vào lớp 10 năm 2020


Chi tiết một số câu hỏi trong đề thi vào lớp môn Toán của trường THPT Chuyên Sư Phạm như sau:
|
BỘ GIÁO DỤC VÀ ĐÀO TẠO TRƯỜNG ĐẠI HỌC SƯ PHẠM HÀ NỘI |
CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM Độc lập - Tự do - Hạnh phúc ĐỀ CHÍNH THỨC |
ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT CHUYÊN NĂM 2020
NĂM HỌC: 2020 - 2021
Môn: Toán
Bài 2. (3,0 điểm)
c) Hai ô tô cùng khởi hành một lúc trên quãng đường từ A đến B dài 120 km. Vì mỗi giờ ô tô thứ nhất chạy nhanh hơn ô tô thứ hai là 10 km nên đến B trước ô tô thứ hai là 0,4 giờ. Tính vận tốc mỗi ô tô, biết rằng vận tốc của mỗi ô tô là không đổi trên cả quãng đường AB.
Bài 3. (1,5 điểm) Bác An muốn làm một cửa sổ khuôn gỗ, phía trên có dạng nửa hình tròn, phía dưới có dạng hình chữ nhật. Biết rằng: đường kính của nửa hình tròn cũng là cạnh phía trên của hình chữ nhật và tổng độ dài các khuôn gỗ (các đường in đậm trong hình vẽ bên, bỏ qua độ rộng của khuôn gỗ) là 8m. Em hãy giúp bác An tính độ dài các cạnh của hình chữ nhật để cửa sổ có diện tích lớn nhất.
Bài 4. (3,0 điểm).
Cho đường tròn (O) và một điểm A nằm ngoài đường tròn. Kẻ tiếp tuyến AB với đường tròn (O) (B là tiếp điểm) và đường kính BC. Trên đoạn thẳng CO lấy điểm I (I khác C và 0). Đường thẳng IA cắt (O) tại hai điểm D và E (D nằm giữa A và E). Gọi H là trung điểm của đoạn thẳng DE.
a) Chứng minh AB.BE = BD.AE.
b) Đường thẳng d đi qua điểm E song song với AO, d cắt BC tại điểm K. Chứng minh HK // CD.
c) Tia CD cắt AC tại điểm P, tia EO cắt BP tại điểm F. Chứng minh tứ giác BECF là hình chữ nhật.
Đáp án đề tuyển sinh vào lớp 10 môn Toán Chuyên Sư Phạm 2020
Bài 1:
a)
\(P = \left( \dfrac{4\sqrt x}{2+\sqrt x} + \dfrac{8x}{4-x} \right): \left( \dfrac{\sqrt x -1}{x-2\sqrt x} - \dfrac{2}{\sqrt x} \right)\)
Với \(x>0 ; x ≠4; x ≠ 9\) ta có:
\(P = \left( \dfrac{4\sqrt x}{2+\sqrt x} + \dfrac{8x}{4-x} \right): \left( \dfrac{\sqrt x -1}{x-2\sqrt x} - \dfrac{2}{\sqrt x} \right)\)
\(= \dfrac{4\sqrt x (2-\sqrt x)+ 8x}{(2+\sqrt x)(2-\sqrt x)}: \dfrac{\sqrt x -1- 2(\sqrt x-2)}{\sqrt x(\sqrt x-2)} \)
\(= \dfrac{4x+8\sqrt x }{(2+\sqrt x)(2-\sqrt x)}: \dfrac{3-\sqrt x }{\sqrt x(\sqrt x-2)} \)
\(= \dfrac{4\sqrt x(\sqrt x+2) }{(2+\sqrt x)(2-\sqrt x)}. \dfrac{\sqrt x(\sqrt x-2)}{3-\sqrt x } \)
\(= \dfrac{4x }{\sqrt x-3}\)
KL....
b)
Ta có:
\(m (\sqrt x - 3) .P > x+1\)
\(\Leftrightarrow m (\sqrt x - 3) . \dfrac{4x }{\sqrt x-3} > x+1\)
\(\Leftrightarrow 4mx > x+1\)
\(\Leftrightarrow x(4m-1) > 1\)
\(\Leftrightarrow 4m-1) > \dfrac{1}{x} \)
Vì x > 0 nên \(\dfrac{1}{x}\) \(<\) < \(\dfrac{1}{9}\)
Do \(4m - 1 > \dfrac{1}{x}\) với ∀ x>9 thì \(4m - 1 ≥ \dfrac{1}{9}\)
\(⇔ 4m ≥ \dfrac{10}{9} ⇔ m ≥ \dfrac{5}{18}\)
Vậy ......
Bài 2
a)
để d1 và d2 song song ⇔
\(\left\{ \matrix{ 5 = m^2 - 4 \hfill \cr 9 ≠ 3m \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ m = ± 3 \hfill \cr m ≠ 3 \hfill \cr} \right.\)
⇒ m = -3
KL....
b)
Ta thấy:
\(\Delta' = (m-1) ^2 - 2m + 5 = m^2 -4m + 6 = (m-2)^2 + 2 > 0 \)
Với mọi m, hay phương trình đã cho luôn có hai nghiệm phân biệt.
Áp dụng hệ thức Vi-ét ta có:
\(\left\{ \matrix{ x_1+x_2 = 2(m-1)\hfill \cr x_1x_2 = 2m - 5 \hfill \cr} \right.\)
Ta có:
\((x_1^2 - 2mx_1 + 2m -1 ) (x_2 - 2) = [x_1^2 - 2(m-1)x_1 + 2m -5 -2x_1+4 ](x_2 - 2)\)
\(= (0 -2x_1+4 )(x_2 - 2) = -2(x_1-2 )(x_2 - 2) = -2 [x_1x_2 - 2(x_1+x_2)+4]\)
\(= -2 [2m-5 - 4(m-1)+4] = 4m - 6\)
Để \((x_1^2 - 2mx_1 + 2m -1 ) (x_2 - 2) \leq 0 \Leftrightarrow 4m - 6 \leq 0 \Leftrightarrow m \leq \dfrac{3}{2}\)
KL....
c.
Gọi vận tốc ô tô thứ nhất là x (km/h, x > 10)
=> vận tốc ô tô thứ hai là x - 10 (km/h)
Theo bài ta có phương trình
\(\dfrac{120}{x-10} - \dfrac{120}{x}=0,4\)
\(0,4x^2 - 4x - 1200 = 0\)
\(\left[ \begin{align}& x = 60 \,\,(t/m) \\& x = -50 \,\,(loại)\\\end{align} \right.\\\)=> vận tốc xe thứ hai là 60 - 10 = 50 km/h
Vậy vận tốc của 2 xe ô tô lần lượt là 60 km/h và 50 km/h
Bài 3.
Gọi chiều dài và rộng của hình chữ nhật lần lượt là a và b (mét, a; b > 0)
Theo giả thiết ta có:
\(P = a+2b + \dfrac{1}2.\pi. 2r = 8\)
\(\Leftrightarrow a+2b + \dfrac{1}2.\pi. a = 8\)
\(\Leftrightarrow \left(\dfrac{\pi}2+1 \right)a+2b = 8\)
\(\Leftrightarrow b =4- \left(\dfrac{\pi+2}4 \right)a\)
Diện tích của cửa sổ là:
\(S = a.b + \dfrac{1}2.\pi. r^2 = a.\left(4- \dfrac{\pi+2}4 .a\right) + \dfrac{\pi}2.\dfrac{a^2}4\)
\(= 4a- \dfrac{\pi+2}4 .a^2+ \dfrac{\pi}2.\dfrac{a^2}4\) \(= 4a + \dfrac{\pi - 2\pi -4}8 .a^2\) \(= 4a - \dfrac{\pi + 4}8 .a^2\)
\(= - \dfrac{\pi + 4}8 \left[ a^2 - \dfrac{32}{\pi+4}.a + \dfrac{16^2}{(\pi+4)^2} \right] + \dfrac{\pi + 4}8.\dfrac{16^2}{(\pi+4)^2}\)
\(= - \dfrac{\pi + 4}8 \left(a - \dfrac{16}{\pi+4} \right)^2 + \dfrac{32}{\pi + 4} \leq \dfrac{32}{\pi + 4} \)
Vậy \({Max}_S= \dfrac{32}{\pi + 4} \Leftrightarrow a = \dfrac{16}{\pi + 4} \Rightarrow b = \dfrac{8}{\pi + 4}\).(thỏa mãn)
KL....
Bài 4.
Hình vẽ:
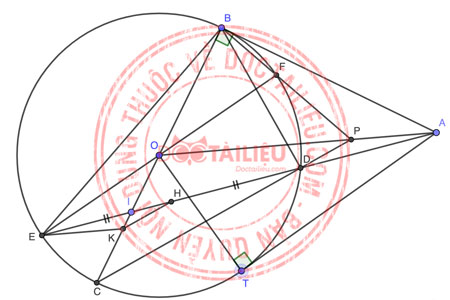
a.
Vì AB là tiếp tuyến của (O) tại B => ∠ABD = ∠BED = ∠BEA (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cũng chẳn cung BD)
Xét △ABD và △AEB có: ∠ABD = ∠BEA (cmt) và ∠BAD chung
=> △ABD ∽△AEB (g.g)
=>\(\dfrac{AB}{AE}=\dfrac{BD}{BE}\)=> AB.BE = AE.BD
b.
Vì AB là tiếp tuyến của (O)=> OA⊥AB=> OBA = 90°. DE là dây cung của (O) mà H là trung điểm của DE
=> OH⊥ DE => ∠OHA = 90°.
Xét tứ giác ABOH có: ∠OHA + ∠OBA = 90° + 90° =180° nên tứ giác ABOH nội tiếp.
=> ∠HAO = ∠HBO (hai góc cùng chắn một cung (1)
Mà EK // AO => ∠KEA = ∠ HAO (hai góc sole trong) (2)
Từ (1) và (2) => ∠KEH = ∠KBH. => Tứ giác HKEB nội tiếp (dấu hiệu tứ giác nội tiếp)
=> ∠EHK = ∠KBE. (3)
Vì tứ giác DCEB nội tiếp => ∠CDE = ∠CBE (hai góc cùng chắn cung CE). (4)
Từ (3) và (4)=> ∠CDE = ∠KHE mà hai góc nằm ở vị trí đồng vị HK // DC.
c.
Xét tứ giác OTAB có OTA+ OBA =180° mà hai góc đối nhau
=> Tứ giác OTAB nội tiếp
=> ∠OAT = ∠OBT (góc nội tiếp cùng chắn cung OI).
Mà trên (O) có: ∠OBT = ∠CBT = ∠CDT (góc nội tiếp cùng chắn cung CT)
=> ∠OAT = ∠ CDT hay ∠PAT = ∠CDT => ∠PAT+ ∠PDT = 180°
Mà hai góc ở vị trí đối nhau trong tứ giác TAPD => TAPD là tứ giác nội tiếp.
=> ∠ATP = ∠ADP (góc nội tiếp cùng chắn cung AP).
Trên (O) có ∠EBC = ∠EDC (góc nội tiếp cùng chắn cung CE).
Mà ∠ADP = ∠EDC (hai góc đối đỉnh)
=> ∠ATP = ∠CBE (1)
AT; AB là tiếp tuyến của (O) => AO là phân giác của góc TAB => ∠TAP = ∠BAP
Xét △TAP và △BAP có:
. AT = AB;
. ∠TAP = ∠BAP (cmt);
. AP chung
=> △TAP và △BAP (c.g.c) (2).
Từ (1) và (2) ∠ABP = ∠EBC
-> EBP = ∠EBC + ∠CBP = ∠ABP+ ∠CBP = ∠CBA 90° => EBF = 90°
Mà EF qua 0, nên EF là đường kính của (O) suy BFCE có 2 đường chéo EF và BC bằng nhau và cắt nhau tại trung điểm mỗi đường nên nó là hình chữ nhật
Bài 5:
Ta có:
\(1 \geq x,y,z > 0\)
⇒ \(1 \geq x^2 \) và \(y \geq xy\) ⇒ \(1 + y + zx \geq x^2 + xy + zx \)
\(\Leftrightarrow \dfrac{x}{1+y+zx} \leq \dfrac{x}{x^2+xy+zx} = \dfrac{1}{x+y+z}\)
Chứng minh tương tự, ta có:
\( \dfrac{y}{1+z+xy} \leq \dfrac{1}{x+y+z}\)
và \( \dfrac{z}{1+x+yz} \leq \dfrac{1}{x+y+z}\)
Cộng vế theo vế, ta có:
\( \dfrac{x}{1+y+zx}+ \dfrac{y}{1+z+xy}+ \dfrac{z}{1+x+yz} \leq \dfrac{3}{x+y+z}\)
(*)Để hệ đã cho có nghiệm ⇔ Dấu bằng của BĐT (*) xảy ra hay x = y = z.
Thay vào ta có:
\(\dfrac{3x}{1+x+x^2}= \dfrac{3}{3x}\)
\(\Leftrightarrow 3x^2= 1+x+x^2\)
\(\Leftrightarrow 2x^2-x-1=0\)
\(\Leftrightarrow \left[ \matrix{ {x} = 1 &(tm) \hfill \cr {x} =-\dfrac{1}2 &(loại) \hfill \cr} \right.\)
⇒ x = y = z = 1. Thử lại thấy đúng.
KL.....
-/-
Các môn thi khác
- Đề thi tuyển sinh vào lớp 10 môn Văn năm 2020 Chuyên Sư Phạm
- Đề thi vào lớp 10 môn Anh năm 2020 Chuyên Sư Phạm Hà Nội
• Điểm chuẩn vào lớp 10 Chuyên Sư Phạm
Trên đây là toàn bộ nội dung của đáp án đề thi tuyển sinh vào lớp 10 môn Toán năm 2020 của Chuyên Sư Phạm được Đọc Tài Liệu thực hiện sau khi kì thi chính thức diễn ra. Với nội dung này các em có thể so sánh đối chiếu kết quả bài thi của mình!
Mong rằng những tài liệu của chúng tôi sẽ là người đồng hành hữu ích với bạn trong kỳ thi này.
